Tomado de https://es.wikipedia.org/wiki/Matriz_(matem%C3%A1ticas)
Matriz (matemáticas)
En matemática, una matriz es un arreglo bidimensional de números. Dado que puede definirse tanto la suma como el producto de matrices, en mayor generalidad se dice que son elementos de un anillo. Una matriz se representa por medio de una letra mayúscula (A,B, …) y sus elementos con la misma letra en minúscula (a,b, …), con un doble subíndice donde el primero indica la fila y el segundo la columna a la que pertenece.
Los elementos individuales de una matriz 






Las matrices se utilizan para múltiples aplicaciones y sirven, en particular, para representar los coeficientes de los sistemas de ecuaciones lineales o para representar transformaciones lineales dada una base. En este último caso, las matrices desempeñan el mismo papel que los datos de un vector para las aplicaciones lineales.
Una matriz es cuadrada si tiene igual numero de filas que de columnas.
MULTIPLICACIÓN DE MATRICES:
Tomado de: https://ekuatio.com/como-multiplicar-matrices/
Cómo multiplicar matrices. Producto de matrices
Para multiplicar dos matrices, se debe cumplir una condición muy importante:
Para definir las dimensiones de una matriz, 2×2, 3×3, 3×2… la primera dimensión hace referencia a las filas de la matriz y la segunda dimensión a las columnas:
![]()
Por tanto, si tenemos una matriz A de m filas y n columnas, sólo la podremos multiplicar por una matriz B que tenga n filas y p columnas (mismo número de columnas de A, que de filas de B):
![]()
La matriz resultante tendrá el mismo número de filas que A y el mismo número de columnas que B.
De todas formas, no tienes que aprenderte esto de memoria para saber cómo multiplicar matrices. Sólo tienes que quedarte con que no se pueden multiplicar cualquier matriz. Siempre deben cumplir la condición anterior y que la matriz resultante, tendrá unas dimensiones distintas a las dos matrices que se multiplican.
Producto de matrices. Ejercicios resueltos
Vamos a ver cómo se realiza el producto de matrices con uno ejercicios.
Ejercicio 1
Sean las matrices A y B las siguientes:

Multiplicar AxB.
En primer lugar, ¿pueden multiplicarse AxB?
Nos tenemos que fijar en las columnas de A y en las filas de B. La matriz A tiene 3 columnas y la matriz B tiene 3 filas. Son iguales y por tanto se pueden multiplicar.

Para multiplicar dos matrices, debemos multiplicar cada fila de la primera matriz, por cada columna de la segunda matriz.
Vamos a verlo paso a paso.
En primer lugar multiplicamos la primera fila de A, por la primera columna de B. Se realiza un producto escalar, es decir, se van multiplicando los elementos de la fila y de la columna y sus resultados se van sumando de la siguiente forma:
El primer elemento de la fila por el primer elemento de la columna…
…más…
el segundo elemento de la fila por el segundo elemento de la columna…
…más…
…el tercer elemento de la fila por el tercer elemento de la columna.
Esta operación, que es el resultado de multiplicar la primera fila por la primera columna, formará primer elemento de la primera fila de la matriz resultante:
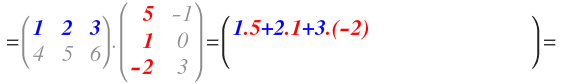
Seguimos multiplicando la primera fila de A por la segunda columna de B. Volvemos a multiplicar cada elemento de la fila, por cada elemento de la columna (primero por primero, segundo por segundo y tercero por tercero) y la operación formará el segundo elemento de la primera fila de la matriz resultante:

Hasta ahora hemos multiplicado la primera fila de A por todas las columnas de B. Con sus resultados, hemos formado la primera fila de la matriz resultante.
Repetimos lo mismo con la segunda fila de A, multiplicándola por cada una de las columnas de B.
Seguimos con la segunda fila de A por la primera columna de B, cuyo resultado formará el primer elemento de la segunda fila:

Y para terminar multiplicamos la segunda fila de A por la segunda columna de B, para formar el segundo elemento de la segunda fila:
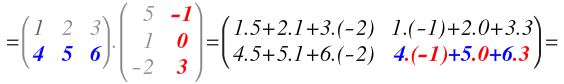
Ahora ya hemos multiplicado todas las filas de A por todas las columnas de B y sólo queda realizar las operaciones que nos quedan en cada elemento:

Date cuenta que las dimensiones de la matriz resultante son distintas de A y de B (tiene las mismas filas que A y las mismas columnas de B).
Ejercicio 2
Calcula los productos posibles entre las siguientes matrices:

Lo que nos piden en este ejercicio es multiplicar las matrices que se puedan multiplicar. Para ello, el número de columnas de la primera matriz debe ser igual al número de filas de la segunda matriz.
Vamos a empezar con la matriz A que tiene 3 columnas. Esta matriz la podremos multiplicar por las matrices que tengan 3 filas. En primer lugar, la podemos multiplicar por la misma matriz A, que también tiene 3 filas.
Realizamos el producto de matrices de A.A=

Multiplicamos filas por columnas:
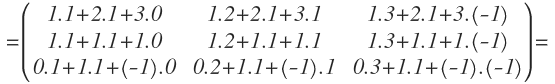
Y operamos:
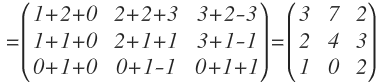
La matriz B también tiene 3 filas, por lo que podemos realizar la multiplicación de A.B=

Multiplicamos filas por columnas y operamos:

Seguimos con la matriz B que tiene 1 columna. La podemos multiplicar por cualquier matriz que tenga 1 fila, pero en este caso no tenemos ninguna, ya que la matriz A tiene 3 filas, la propia matriz B tiene 3 filas y la matriz C tiene 2 filas. Por tanto, la matriz B no la podemos multiplicar por ninguna matriz.
Por último vamos a ver los posibles productos de matrices con la matiz C. La matriz C tiene 3 columnas, por lo que la podemos multiplicar por matrices que tengan 3 filas.
La matriz A tiene 3 filas, por lo multiplicamos C.A:

Multiplicamos filas por columnas:

Y operamos:
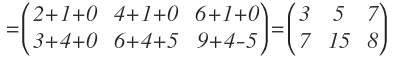
La matriz C también se puede multiplicar por la matriz B, que tiene 3 filas:

Multiplicamos filas por columnas y operamos:

Ahora que ya sabes cómo multiplicar matrices, vamos a ver las propiedades del producto de matrices cuadradas.
Propiedades de la multiplicación de matrices cuadradas
1- El producto de matrices cuadradas cumple la propiedad asociativa
![]()
2- El elemento neutro es la matriz identidad
Cualquier matriz multiplicada por la matriz identidad dará como resultado la misma matriz. La matriz identidad es como si fuera el 1 para los números.
3- La multiplicación de matrices no es conmutativa en general.
Por norma general, la multiplicación de A por B no tiene el mismo resultado que B por A
![]()
Puede existir el caso de que A.B=B.A, pero no es lo normal.
4- Es distributiva respecto de la suma
![]()
5- El producto de dos matrices no nulas puede ser una matriz nula.
Por ejemplo:

6- Dada una matriz cuadrada A, no siempre existirá una matriz inversa que cumpla:
![]()
Tomado de: https://aga.frba.utn.edu.ar/matriz-asociada-a-una-transformacion-lineal/
Matriz asociada a una transformación lineal.
Ejemplos introductorios
Ejemplo 1
Sea la siguiente transformación lineal:¿Existirá una matriz que multiplicada por dé por resultado ? Para esto vamos a escribir los vectores como columna:
¿Cuál debería ser el tamaño de la matriz?
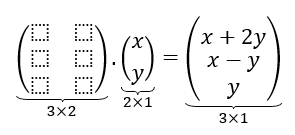
Efectuando el producto de matrices, podemos obtener los coeficientes de :
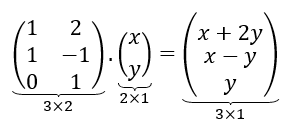
Encontramos una matriz que realiza la transformación lineal. Se conoce como la matriz estándar de la transformación lineal.
Notemos que la transformación va de a , y que el orden de la matriz es .
Ejemplo 2
Ahora consideremos la siguiente transformación lineal:
Queremos buscar una matriz tal que:
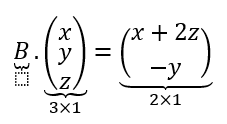
Pensando el orden de la matriz y el valor de sus elementos llegamos a:
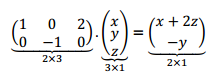
Hemos hallado de manera intuitiva la matriz estándar de la transformación lineal. Notemos que la transformación va de a y que el orden de la matriz asociada a la transformación lineal es .
Inversa de una matriz 2 x 2:



