CLASE DERIVACIÓN IMPLICITA, LOGARITMICA Y REGLA DE L´HOPITAL

Derivación Implícita

(http://www.sectormatematica.cl/seccion/derivacion.htm)

Funciones explícitas y funciones implícitas

En los cursos de cálculo la mayor parte de las funciones con que trabajamos están expresadas en forma explícita, como en la ecuación

dónde la variable y está escrita explícitamente como función de x. Sin embargo, muchas funciones, por el contrario, están implícitas en una ecuación. La función y = 1 / x, viene definida implícitamente por la ecuación: x y = 1.

Si queremos hallar la derivada para esta última ecuación, lo hacemos despejando y, así, y = 1 / x = x ^-1, obteniendo su derivada fácilmente: .

El método sirve siempre y cuando seamos capaces de despejar y en la ecuación. El problema es que sino se logra despejar y, es inútil este método. Por ejemplo, ¿cómo hallar dy/dx para la ecuación x²- 2y³+ 4y = 2, donde resulta muy difícil despejar y como función explícita de x?

El método de regla de la cadena para funciones implícitas

Ya sabemos que cuando se derivan términos que solo contienen a x, la derivación será la habitual. Sin embargo, cuando tengamos que derivar un término donde aparezca la y, será necesario aplicar la regla de la cadena.

Ejemplo 1:

Aquí las variables coinciden: se deriva normalmente.

Ejemplo 2:

Aquí las variables no coinciden: se usa regla de la cadena.

Ejemplo 3:

Hallar , de la función implícita:

Aplicando la notación , a cada término y extrayendo las constantes;

.

En el primer término las variables coinciden, se deriva normalmente, en el segundo término se aplica la derivada de un producto (primer paréntesis cuadrado), lo mismo en el tercer término.

.

La regla de la cadena se aplica el término , como puede observarse a continuación claramente en el segundo paréntesis,

quitando paréntesis y ordenando los términos,

,

pasando algunos términos al lado derecho,

extrayendo el factor común ,

y finalmente despejando, obtenemos la respuesta requerida:

DERIVACIÓN LOGARITMICA

(tomado de:http://calculo.cc/temas/temas_bachillerato/primero_ciencias_sociales/funciones_derivadas/teoria/derivada_pot_exp.html)

Pasos de la derivación logarítmica

1) Se toman logarítmos neperianos de ambos lados de la ecuación y = f(x)

y se utilizan las propiedades de los logarítmos para simplificar.

2) Se deriva implicitamente con respecto a la variable x .

3) Se despeja de la ecuación resultante y' .

Ejemplo de derivación logarítmica:

derivacion logaritmica

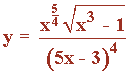
En primer lugar tomamos logarítmos neperianos en ambos miembros:

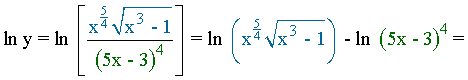
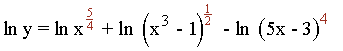
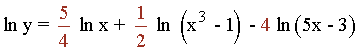
derivacion logaritmica

En segundo lugar se derivan ambos miembros:

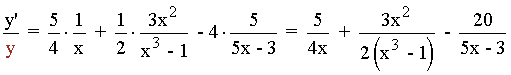
derivacion logaritmica

En tercer lugar se despeja y ' :

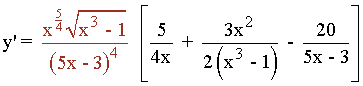
derivacion logaritmica

Funciones potenciales exponenciales

A veces es necesario tomar logarítmos para el cálculo de funciones

potenciales exponenciales, es decir, que tienen x en la base y en

el exponente.

Ejemplo de función potencial exponencial:

En primer lugar tomamos logarítmos neperianos en ambos miembros:

En segundo lugar se derivan ambos miembros:

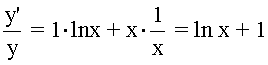
derivada funcion potencial exponencial

En tercer lugar se despeja y ' :

REGLA DE L´HOPITAL E INDETERMINACIONES ${\frac {0}{0}}\qquad {\frac {\infty }{\infty }}\qquad 0\cdot \infty \qquad 1^{\infty }\qquad 0^{0}\qquad \infty ^{0}\qquad +\infty -\infty$ .

(Tomado de: http://www.vitutor.com/fun/6/lopital.html)

Un estudio mas completo sobre estas indeterminaciones lo encuentras en: http://www.vitutor.com/fun/3/a_11.html

Si:

f y g , en donde f y g son derivables en un entorno de a y existe límite , entonces este límite coincide con límite .

regla de L'Hôpital

Para aplicar la regla de L'Hôpital hay que tener un límite de la forma límite , donde a puede ser un número o infinito, y aparecer las indeterminaciones: