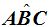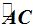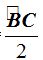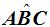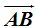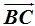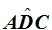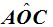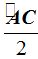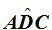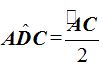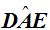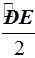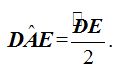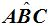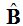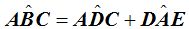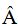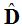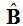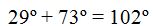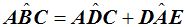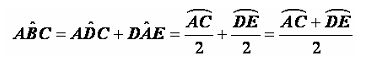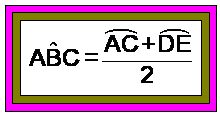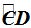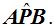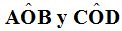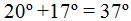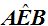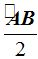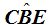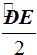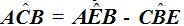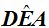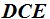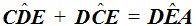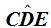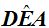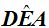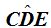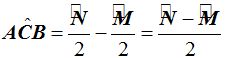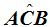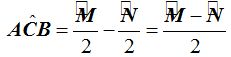Ángulos en la Circunferencia
En este capítulo aprenderemos los diferentes tipos de ángulos que están asociados a la circunferencia. Cada uno se puede tomar como una propiedad y se suele aplicar mucho en los ejercicios y problemas de ángulos en la circunferencia.
Veamos a continuación cada uno de ellos:
1. Ángulo Central
El ángulo central, cuyo vértice se encuentra en elcentro de la circunferencia«O», sus lados son dos radios.

«La medida del ángulo central es igual a la medida del arco comprendido entre sus lados».
2. Ángulo Inscrito
En este caso el vértice se encuentra sobre la circunferencia, el punto «B» y sus lados son dos cuerdas.

«La medida del ángulo inscrito es igual a la mitad de la medida del arco comprendido entre sus lados».
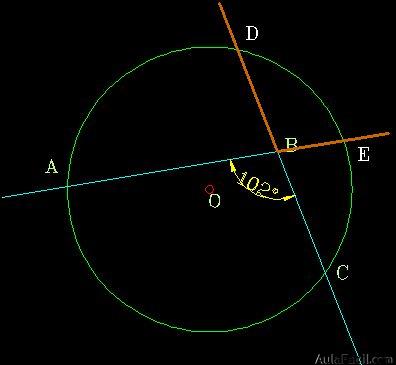
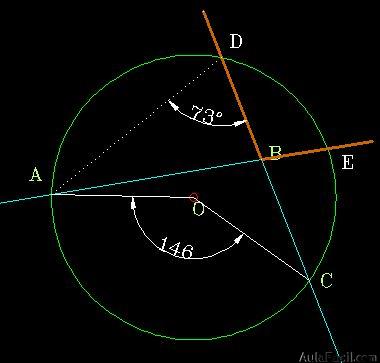
3. Ángulo Semi-Inscrito
En este ángulo, el vértice se encuentra sobre la circunferencia, sus lados son una tangente y una cuerda.

«La medida del ángulo semi-inscrito es igual a la mitad del arco correspondiente a la cuerda».
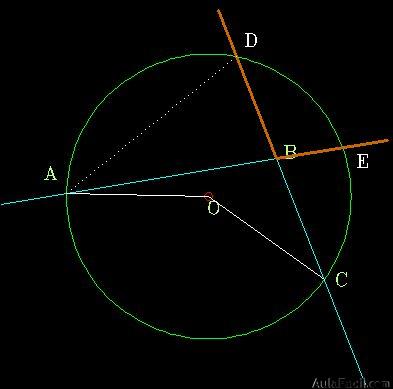
4. Ángulo Ex-Inscrito
El vértice de este tipo de ángulo se encuentra sobre la circunferencia.

«El ángulo ex-incrito es el ángulo adyacente y suplementario del ángulo inscrito».
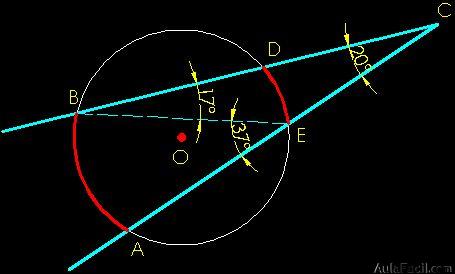
5. Ángulo Exterior
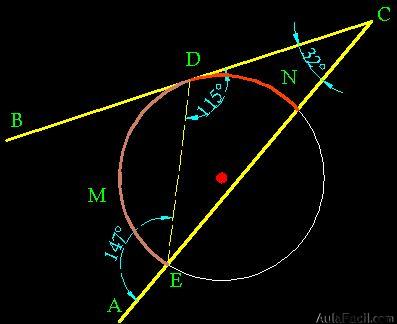
El vértice del ángulo exterior se encuentra en la zona exterior a la circunferencia, sus lados pueden ser dos segmentos secantes, dos tangentes o una secante y una tangente.
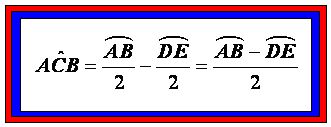
«La medida del ángulo exterior es igual a la semidiferencia de los arcos formados por los lados».
Véase las siguientes figuras:
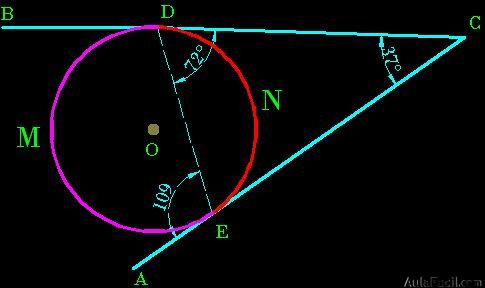
Caso I: Ángulo entre Dos Secantes:

Caso II: Ángulo entre Dos Tangentes:

Caso III: Ángulo entre una Recta Tangente y otra Secante:

Ejercicios Resueltos
Aprenda como resolverejercicios de ángulos en la circunferenciaaplicando las propiedades y teoría vista.
Ejercicio 01:
Calcular x en la siguiente figura. Si «A» y «B» son puntos de tangencia.

Resolución:
En este ejercicio aplicaremos las fórmulas del ángulo inscrito y exterior de la circunferencia, veamos:

– Por ángulo inscrito: Arco AB = 2(60°) = 120°
– Por ángulo exterior en APC: x + 120° = 180°
∴ x = 60°
Ejercicio 02:
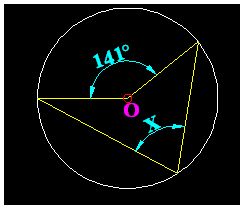
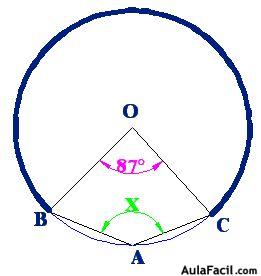
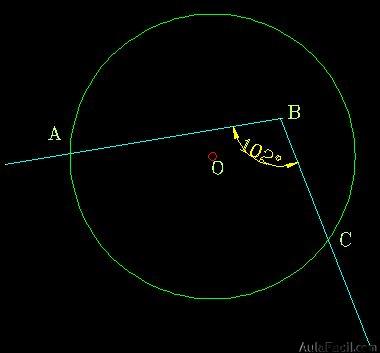
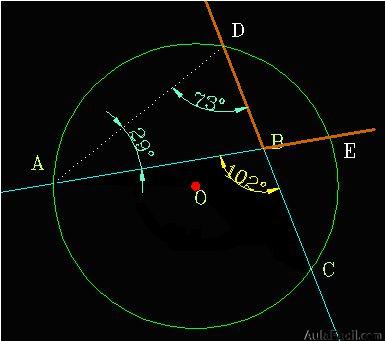
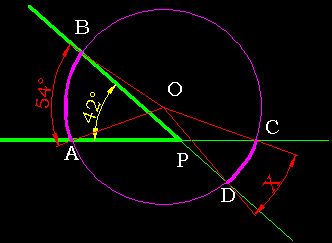
Hallar «x», si «O» es centro de la circunferencia.

Resolución:
Trazamos el radio OB para formar el ángulo central en la circunferenciay a la vez el triángulo AOB.

- Por ángulo central: m∡AOB = arco AB = 140°.
- El triángulo AOB estriángulo isósceles, entonces trasladamos el ángulo «x».
Por último, aplicamospropiedad de triángulosen el Δ AOB: «suma de ángulo internos»
⇒ x + x + 140 = 180°