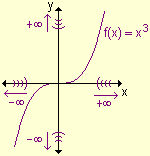Tomado de: https://www.fca.unl.edu.ar/Limite/contenidos.htm
En este link puedes estudiar el tema completo:
https://www.fca.unl.edu.ar/Limite/2.0%20L%EDmite%20de%20funciones.htm
Límites infinitos
Analicemos, a partir de su gráfica, la existencia de los límites.
|
|
|
|
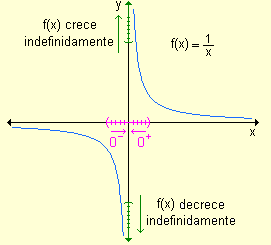
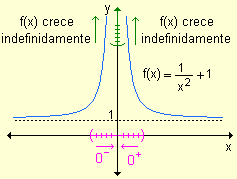
Las dos ramas de la curva se acercan cada vez más al eje y a medida que x se aproxima a cero. Para esta gráfica la recta x = 0 es asíntota vertical. |
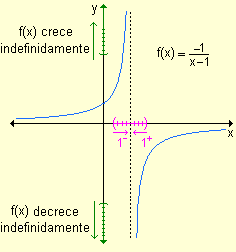
Las dos ramas de la curva se acercan cada vez más a la recta x = 1 a medida que x se aproxima a ese valor. Para esta gráfica la recta x = 1 es asíntota vertical. |
 
|
 
|
|
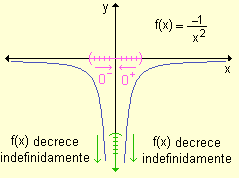
Para esta gráfica la recta x = 0 es asíntota vertical. |
Para esta gráfica la recta x = 0 es asíntota vertical. |
El comportamiento de estas funciones no puede describirse con la idea y el concepto de límite que se ha estudiado hasta ahora.
Analizando nuevamente la función y = 
, se observa en la gráfica que cuando x ® 0+, los valores de f crecen más allá de todo tope. Por lo tanto f no tiene límite cuando x ® 0+. Sin embargo resulta conveniente decir que f(x) se aproxima a ¥ cuando x ® 0+. Se escribe 
.
Esto no significa que el límite existe ni que +¥ es un número real, sino que expresa que la función se hace tan grande como deseamos escogiendo x suficientemente cercano a cero.
Resumen
| Simbólicamente se escribe: | Gráficamente: |
|
|
|
|
|
|
|
|
|
|
|
|
para indicar que los valores de la función crecen indefinidamente (sin tope) cuando x se acerca a "a" por izquierda y por derecha.
para indicar que los valores de la función decrecen indefinidamente (sin tope) cuando x se aproxima a "a" por valores menores y mayores que él.
para indicar que los valores de la función crecen indefinidamente cuando x se aproxima a "a" por valores menores que él.
para indicar que los valores de la función decrecen indefinidamente cuando x se aproxima a "a" por valores mayores que él.
para indicar que los valores de la función decrecen indefinidamente cuando x se acerca a "a" por valores menores que él.
para indicar que los valores de la función crecen indefinidamente cuando x se acerca a "a" por valores mayores que él.Nota. Cuando se refiere a límites infinitos en realidad no son límites sino que proporcionan símbolos y un lenguaje útiles para describir el comportamiento de funciones cuyos valores se hacen arbitrariamente grandes (positivos o negativos).
Ejemplo. Sea la gráfica
de la función f(x) = 
:
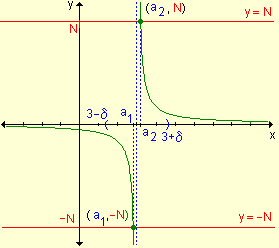
Observando la gráfica se puede escribir: 
y 
Ejemplos. Determine los siguientes límites
a) 
b) 
c) 
a) 
Cuando x ® 3 el denominador tiende a cero y la expresión tiende a ¥ .
Cuando x se aproxima a 3 por derecha, la expresión 
es negativa pues el numerador es negativo y cada uno de los factores del denominador es positivo. Por lo tanto, el límite es -¥ .
b)= 
Cuando x ® 3 el denominador tiende a cero y la expresión tiende a ¥ .
Cuando x se aproxima a 3 por izquierda, la expresión es positiva, pues el numerador es negativo, el factor (x + 3) es positivo y (x - 3) negativo. Por lo tanto, el límite es +¥ .
c) El límite para x ® 3 no existe.
Límites en el infinito
Analizaremos el comportamiento de las funciones definidas gráficamente cuando x crece indefinidamente y cuando x decrece indefinidamente
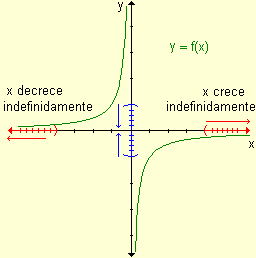
a) Si x crece indefinidamente la función f(x) se acerca a 0. b) Si x decrece indefinidamente, los valores de la función se acercan a 0. |
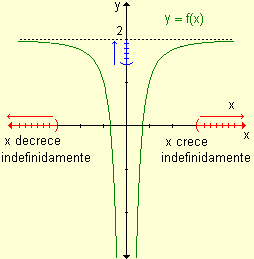
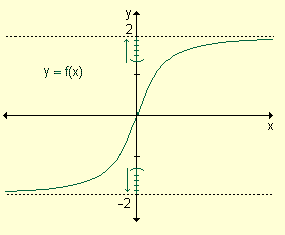
a) Si x crece indefinidamente la función f(x) se acerca a 2. b) Si x decrece indefinidamente, los valores de la función se acercan a 2. |
|
La recta y = 0 es asíntota horizontal de la función. |
La recta y = 2 es asíntota horizontal de la función. |
a) Si x crece indefinidamente la función f(x) se acerca a 2. b) Si x decrece indefinidamente, los valores de la función se acercan a -2. |
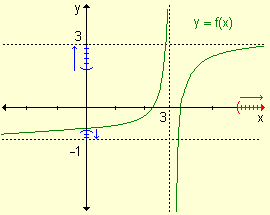
a) Si x crece indefinidamente la función f(x) se aproxima a 3. b) Si x decrece indefinidamente, los valores de la función se aproximan a -1. |
|
Las rectas y = 2 e y = -2 son asíntotas horizontales de la función. |
Las rectas y = 3 e y = -1 son asíntotas horizontales de la función. |
En el primer ejemplo anotamos 
.
Recordemos que ¥ no representa un número. La expresión anterior expresa que el límite de f(x) cuando x crece o decrece indefinidamente es cero.
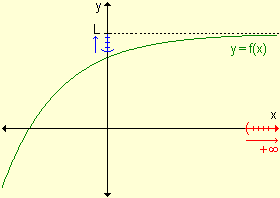
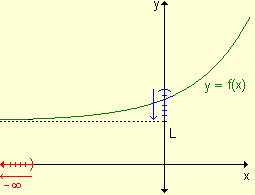
El comportamiento de funciones que se aproximan a un número cuando la variable crece o decrece indefinidamente (x ® +¥ , x ® -¥) se indica de la siguiente manera:
|
Simbólicamente se escribe |
Gráficamente: |
|
|
|
|
|
|
para indicar que la función tiende a L cuando los valores de x crecen indefinida- mente.
para indicar que la función tiende a L cuando los valores de x decrecen indefinidamente.Formalizando la definición de límite de una función que tiende a un número finito cuando la variable independiente tiende a +¥ ó a -¥, resulta:
Definición.
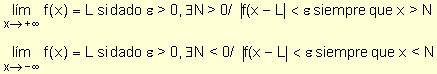
Las propiedades referidas al álgebra de límites válidas si "x® a" se cumplen también si "x® +¥ " y "x® –¥".
Ejemplo. Calcule 
.
Cuando x toma valores grandes, es pequeño. Tomando x suficientemente grande, puede hacerse tan pequeño como queramos. Por lo tanto 
.
Por otra parte 
y como el límite de la diferencia es la diferencia de los límites resulta: = 3 – 0 = 3
Problema. Se proyecta que dentro de t años, la población de cierto pueblo será p(t) = 
miles de personas. ¿Qué se espera que suceda con la población
a medida que el tiempo transcurre indefinidamente?
Solución. Para determinar el comportamiento de la función cuando el tiempo transcurre
indefinidamente se debe calcular el límite
.
Cuando t ® +¥ , también t +1® +¥ y, por lo tanto, 
® 0.
En consecuencia = 20. Esto expresa que a medida que el tiempo transcurre, la población tiende a estabilizarse en 20 000
personas.
Límites infinitos en el infinito
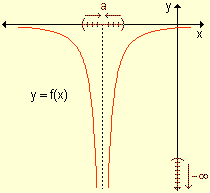
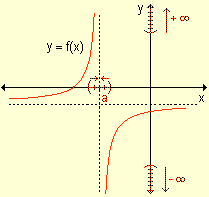
En la siguiente tabla se presenta el análisis del comportamiento de funciones que crecen o decrecen indefinidamente cuando la variable también crece o decrece sin tope.
|
|
|
|
|
Estas funciones presentan comportamientos que no pueden describirse con la idea y el concepto de límite estudiado. Por lo tanto, debe extenderse dicho concepto para interpretar y simbolizar estas situaciones.
|
Simbólicamente se escribe: |
Gráficamente |
|
|
|
|
|
|
|
|
|
|
|
|
para indicar que la función decrece indefinidamente cuando la variable crece indefinidamente.
para indicar que la función crece indefinidamente cuando la variable decrece indefinidamente.
para indicar que la función decrece indefinidamente cuando la variable decrece.
para indicar que la función crece indefinidamente cuando la variable crece.
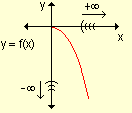
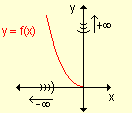
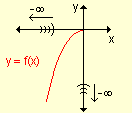
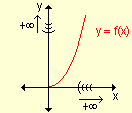
Recordemos que en cualquiera de los límites
, 
, 
, 
, es importante tener en cuenta que +¥ o -¥ no son números. En estos casos se dice que el límite no existe.
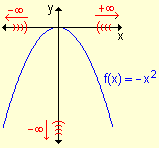
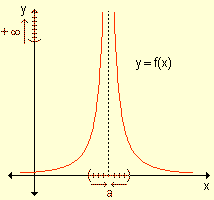
La expresión significa que si x ® +¥ ; f(x) ® +¥ .
Es decir que para todo M > 0, existe k > 0 tal que si x > k, Þ f(x) > M. Esto significa que si x es positivo y grande, su correspondiente imagen f(x) también es positiva y grande.
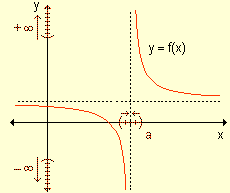
Ejemplo. Discuta el comportamiento de la función y = 
para
x ® +¥ y para x ® -¥ . Grafique.
Cuando x ® +¥ , x3 ® +¥ y por lo tanto ® +¥ . Se puede
escribir 
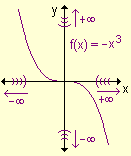
Cuando x ® –¥ , x3 ® –¥ y por lo tanto ® –¥ .
Luego
Su gráfica es
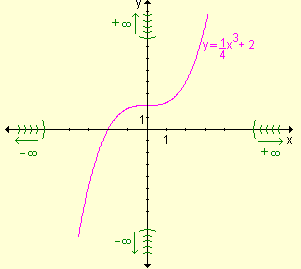
Un límite importante
Se puede demostrar que 
Al evaluar el numerador y el denominador en x = 0, se obtiene la
indeterminación 
. Para resolverlo, no pueden utilizarse las técnicas vistas
anteriormente, pero sin embargo, el 
existe y vale 1.
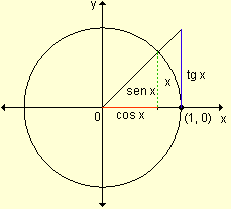
Sea un ángulo cuya medida en radianes sea x, 0 < x < 
.
|
Observando la gráfica resulta:
sen x < x < tg x Como sen x ¹ 0, dividiendo por sen x se obtiene:
Dado que
resulta: 1 < |
|
,
Por lo tanto: 
Þ 
Si se hace tender x a cero, 
y al estar 
comprendido entre dos expresiones que tienden a 1 cuando x ® 0, también deberá
tender a 1. Por lo tanto: 
.
Para que esta demostración pueda generalizarse falta analizar qué es lo que ocurre para valores negativos de x.
Se designa con (- x) a los valores negativos de x.
Como senx es una función impar, sen(-x) = -senx.
Por lo tanto: 
Þ 
Nota. El
cociente 
es tanto más cercano a 1 cuanto más próximo a 0 se considere el
valor de x.
| Esto permite geométricamente interpretar que para medidas de arco muy pequeñas, sus correspondientes valores de sen x son aproximadamente iguales a x. |
|
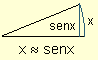
Ejemplo. Halle el valor
de 
Al evaluar numerador y denominador en cero, resulta la indeterminación . Para resolver este límite, se trata de escribir el cociente de manera tal de poder aplicar el teorema anterior: 
Por propiedad de límite, 
Además, si x ® 0, 2x también tiende a cero y por lo tanto: 
En consecuencia, 
Ejemplo. Calcule el valor de 
Sustituyendo la variable por 0 resulta una indeterminación.
Utilizando la identidad 
es
posible transformar el cociente de manera tal de poder aplicar el teorema anterior.
Por lo tanto: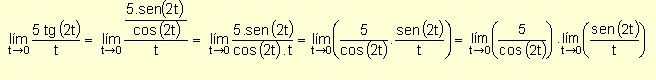 
Hallando el primer límite 
En el segundo límite multiplicamos y dividimos por 2 y teniendo en cuenta que si t ® 0 también 2t ® 0 resulta que: 
Entonces: 
= 5.2 = 10
Ejemplo. Halle
Reemplazando la variable por el valor al cual tiende resulta la indeterminación .
Aplicando diferencia de cuadrados en el denominador y teniendo en cuenta que si x tiende a 3 entonces x - 3 tiende a 0 resulta:
La indeterminación 
Para salvar indeterminaciones de este tipo, es posible reducir el cociente planteado a otro cuyo denominador no sea cero factorizando el numerador y/o el denominador, cancelando luego los factores comunes. En otras ocasiones, es posible crear un factor común multiplicando el numerador y el denominador por la expresión conjugada de la que se presenta en uno de ellos.
Ejemplo. Halle 
Al sustituir, resulta 
y 
lo que genera una
indeterminación del tipo .
Sin embargo, como 
si x ¹ 3, resulta que la función 
coincide con la función (x + 3) salvo en x = 3.
Como interesa analizar el comportamiento de la función para valores de x próximos a 3 (por izquierda y por derecha), es posible determinar el
comportamiento de analizando el de la función (x
+ 3).
Por lo tanto puede decirse que 
Nota. Existe algo sospechoso en este ejemplo. Si el 3 no estaba en el dominio antes de simplificar, pero sí lo estaba después de simplificar, la función seguramente ha cambiado.
Al decir 
mentimos un poco. Lo que en realidad quisimos decir es que esas dos expresiones son iguales en donde están definidas. En realidad 
y x + 3 son distintas. La diferencia entre ellas es que
x = 3 no pertenece al dominio de pero sí al dominio de x + 3. Puesto que 
ignora cualquier valor que f pueda tomar x = 3, eso
no interesa. Desde el punto de vista del límite en 2 esas funciones sí son iguales.
Ejemplo. Calcule el
valor de 
.
Al sustituir la variable por 1, tanto el numerador como el denominador se anulan y se genera la indeterminación 
. Se factorizan el numerador y el denominador y, para
x ¹ 1, se simplifican los factores comunes:
Ejemplo. Halle el valor
de 
.
Reemplazando la variable por 3 se obtiene la indeterminación . Para resolver este límite, se racionaliza el denominador multiplicando el numerador y el denominador por la expresión
conjugada de la del denominador y resulta:
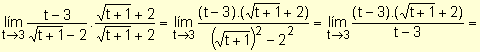
Ejemplo. Determine el límite 
.
Al sustituir, resulta 
y 
lo que genera una
indeterminación del tipo .
Si x ® 3, el denominador tiende a cero. Si x se aproxima a 3 por derecha o por izquierda, en cualquiera de los casos el denominador es positivo por estar elevado al cuadrado. Como el numerador negativo (-1), se concluye que el límite es -¥.
La indeterminación 
Se analizará el límite del cociente de dos funciones polinomiales en el que la variable crece o decrece indefinidamente. Se debe tener en cuenta que el límite de una función polinomial de grado n ³ 1 cuando x tiende a +¥ ó a -¥ es +¥ ó -¥ . Para resolver límites de este tipo, se dividen el numerador y el denominador de la función dada por xn, siendo n el mayor de los grados de las funciones polinomiales. Luego se aplican las propiedades de los límites.
Ejemplo. Halle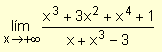 
La función dada consiste en el cociente de dos funciones polinomiales: una de grado 4 y otra de grado 3. Por lo tanto, se dividen el numerador y el denominador por x4 y resulta:
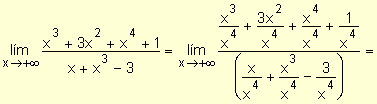
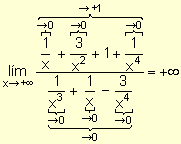
En el ejemplo dado, el grado de la función polinomial del numerador es mayor que el de la del denominador y se obtuvo en este caso ¥.
Ejemplo. Determine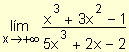 
Se dividen el numerador y denominador por x3:
.
Puede observarse que el ejemplo se refiere al cálculo del límite del cociente de dos funciones polinomiales del mismo grado y se obtuvo como resultado el cociente de los coeficientes de los términos de mayor grado de ambas.
Ejemplo. Calcule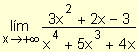 
.
Se dividen el numerador y denominador por x4:
En este ejemplo, el grado de la función polinomiales del numerador es menor que el de la del denominador y se obtuvo como resultado cero.
Nota. Al
calcular
, donde p(x) y q(x) son dos funciones
polinomiales, se obtiene:
a) el cociente de los coeficientes de los términos de mayor grado de la función polinomial del numerador y la del denominador, si ambas tiene el mismo grado.
b) +¥ ó –¥ si el grado de la función polinomial del numerador es mayor que el de la del denominador.
c) 0 si el grado de la función polinomial del numerador es menor que el de la del denominador.
Problema. Un tanque
contiene 5000 litros de agua pura. Se bombea al tanque salmuera que contiene 30 gramos de sal por litro de agua, a razón de 25 
. La concentración de sal después de
t minutos es: C(t) = 
(en 
).
a) ¿Cuánto tiempo tiene que
transcurrir para que la concentración sea de 10 ?
b) ¿Qué sucede con la concentración cuando el tiempo transcurre indefinidamente?
Solución
a) Para determinar el tiempo
que debe transcurrir para que la concentración sea de 10 , se debe igualar la concentración a 10.
10 = Þ 2000 + 10t = 30t Þ 20t = 2000 Þ t = 100
Es decir, a los 100 minutos la concentración será de 10.
b) Para analizar el
comportamiento de la concentración cuando el tiempo transcurre indefinidamente, se debe encontrar el límite cuando t ® +¥ , es decir 
. Como es un cociente de dos funciones polinomiales, se dividen el
numerador y el denominador por t y se obtiene:
Cuando t ® +¥ la concentración tiende a 30 
.
La
indeterminación 
Los procedimientos algebraicos para salvar una indeterminación de este tipo, se desarrollan en los siguientes ejemplos:
Ejemplo. Determine el valor de 
.
Al reemplazar la variable por 2 resulta ¥ -¥ , que es una indeterminación.
Resolviendo la diferencia se obtiene:
Cuando x se aproxima a 2 por derecha, el numerador tiende a –3 y el denominador a 0 por valores mayores que él. Por lo tanto, la expresión resulta negativa y el límite es -¥.
= -¥
Ejemplo. Calcule 
No es posible escribir
= ¥ - ¥ , ya que esa diferencia es indeterminada.
Se expresa la función polinomial de la siguiente manera: 
= –¥ ya que x ® +¥ y (2 – x3)® –¥
Ejemplo. Halle 
(indeterminado)
La expresión 
Por lo tanto: 
La indeterminación 
Para salvar una indeterminación de este tipo, se pueden realizar distintos procedimientos algebraicos. Algunos de ellos se desarrollan en los siguientes ejemplos.
Ejemplo. Halle 
Cuando x ® –3, x2 + 6x +9 ® 0 y 
, por lo tanto 
, indeterminado.
Sin embargo, 
si x ¹ - 3.
Por lo tanto: 
Ejemplo. Calcule 
Como 
y 
, resulta 
, indeterminado.
En este caso = 
, si x ¹ 0.
Ejemplo. Halle 
, indeterminado, ya que
y 
.
Sin embargo, 
si x ¹ 2.
Por lo tanto: 
ASINTOTA OBLICUAS
Las asíntotas oblicuas son rectas de ecuación:
Sólo hallaremos las asíntotas oblicuas cuando no haya asíntotas horizontales.
Ejemplos
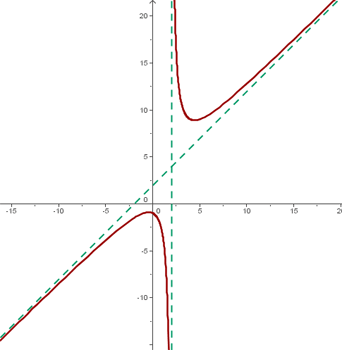
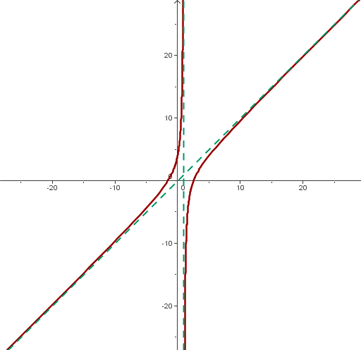
TOMADO DE
https://www.fca.unl.edu.ar/Continuidad/3.0%20Funci%F3n%20continua.htm
Función continua
"Es verdad que un matemático que no tenga algo de poeta nunca será un matemático perfecto." (F. Weirstrass)
En la naturaleza y en nuestra vida diaria aparecen numerosos fenómenos que tienen un comportamiento continuo. Por ejemplo, el crecimiento de una planta es continuo, el desplazamiento de un vehículo o el volumen del agua que fluye de un recipiente. Pero también se presentan discontinuidades en muchas situaciones, como las corrientes eléctricas.
Muchos procesos físicos son continuos, tantos que durante los siglos XVIII y XIX a pocos se les ocurrió buscar otro tipo de comportamiento. Recién alrededor de 1920 descubrieron que los átomos que vibran en una molécula de hidrógeno pueden oscilar sólo en niveles de energía discretos y que los átomos al ser calentados, emiten luz en frecuencias discretas y no en espectros continuos. Como resultado de estos descubrimientos y dado que en informática y en estadística hacen un intenso uso de funciones discretas, la continuidad ha adquirido una gran importancia.
Intuitivamente se puede pensar en una función continua en un punto si se puede dibujar su gráfica cerca del punto sin levantar el lápiz del papel. De la misma manera, se puede decir que una función es discontinua en un punto, si se debe levantar el lápiz del papel para obtener la gráfica de la función a ambos lados del punto indicado.
La definición matemática de continuidad responde al significado de la palabra continuidad en el lenguaje cotidiano. Se puede pensar que un proceso continuo tiene lugar gradualmente, sin interrupciones ni cambios abruptos.
| Continuidad de una función en un punto | Tipos de discontinuidades | Función continua en un intervalo | Teoremas de las funciones continuas |
Si quiere probar sus conocimientos a continuación se presentan ejercicios y problemas que integran todos los temas.
| Ejercicios integradores | Problemas de aplicación | Prueba de opción múltiple | Más ejercicios |