Tomado de:

https://es.khanacademy.org/science/physics/torque-angular-momentum/torque-tutorial/a/rotational-inertia

 

¿Qué es la inercia rotacional?

La inercia rotacional es una propiedad de cualquier objeto que puede girar. Es un valor escalar que nos indica qué tan difícil es cambiar la velocidad de rotación del objeto alrededor de un eje de rotación determinado.
En mecánica rotacional, la inercia rotacional desempeña un papel similar al de la masa en la mecánica lineal. De hecho, la inercia rotacional de un objeto depende de su masa. También depende de la distribución de esa masa respecto al eje de rotación.
Cuando una masa se aleja del eje de rotación se hace cada vez más más difícil cambiar la velocidad de rotación del sistema. Intuitivamente, esto es porque la masa lleva consigo más momento alrededor del círculo (debido a la velocidad más alta) y porque el vector de momento cambia más rápidamente. Estos dos efectos dependen de la distancia desde el eje.
La inercia rotacional se denota con el símbolo I. Para un solo cuerpo como el de una pelota de tenis de masa m que gira en un radio r desde el eje de rotación (ver la Figura 1), la inercia rotacional es
I, equals, m, r, squared
y, en consecuencia, la inercia rotacional en el SI tiene unidades de k, g, dot, m, squared.
A la inercia rotacional comúnmente se le conoce como el momento de inercia. También a veces se le llama el segundo momento de la masa; aquí 'segundo' se refiere al hecho de que depende de la longitud del brazo del momento al cuadrado.
Figura 1: una pelota de tenis atada que gira alrededor de un punto central

¿Cómo se relaciona la inercia rotacional con la segunda ley de Newton?

La inercia rotacional toma el lugar de la masa en la versión rotacional de la segunda ley de Newton.
Considera una masa m unida a un extremo de una barra sin masa. El otro extremo de la barra está articulado para que el sistema pueda girar alrededor de la bisagra central como se muestra en la figura 2.
Figura 2: una masa que rota debido a una fuerza tangencial
Ahora comenzamos a rotar el sistema al aplicar una fuerza tangencial F, start subscript, T, end subscript a la masa. De la segunda ley de Newton,
F, start subscript, T, end subscript, equals, m, a, start subscript, T, end subscript.
Esto también se puede escribir como
F, start subscript, T, end subscript, equals, m, left parenthesis, r, alpha, right parenthesis.
La segunda ley de Newton relaciona la fuerza con la aceleración. En la mecánica rotacional tau toma el lugar de la fuerza. Al multiplicar ambos lados por el radio obtenemos la expresión deseada.
\begin{aligned} F_T r &= m (r \alpha) r\\ \tau &= m r^2 \alpha \\ \tau &= I \alpha\end{aligned}
Ahora esta expresión puede utilizarse para encontrar el comportamiento de una masa en respuesta a una torca conocida.
Ejercicio 1a:
Un motor capaz de producir una torca constante de 100, space, N, m y una velocidad de rotación máxima de 100, space, N, m se conecta a un volante con inercia rotacional de 0, comma, 1, space, k, g, m, squared. ¿Qué aceleración angular experimentará el volante cuando se enciende el motor? 
Solución
Al reacomodar la versión rotacional de la segunda ley de Newton y sustituir los números encontramos:
\begin{aligned} \alpha &= \frac{\tau}{I} \\ &= \frac{100~\mathrm{Nm}}{0{,}1~\mathrm{kg m^2}} \\ &= 1000 ~\mathrm{rad/s^2}\end{aligned}
Ejercicio 1b:
¿En cuánto tiempo el volante tendrá una velocidad constante si parte del reposo? 
Al usar cinemática rotacional,
omega, equals, omega, start subscript, 0, end subscript, plus, alpha, t
Ya que sabemos la velocidad de rotación máxima del motor, podemos encontrar el tiempo que lleva acelerar hasta esa velocidad rotacional.
\begin{aligned} t &= \frac{\omega_\mathrm{max}}{\alpha} \\ &= \frac{150~\mathrm{rad/s}}{1000~\mathrm{rad/s^2}} \\ &= 0{,}15~\mathrm{s}\end{aligned}

¿Cómo podemos calcular la inercia rotacional en general?

Los sistemas mecánicos a menudo están hechos de muchas masas interconectadas, o formas complejas.
Es posible calcular la inercia rotacional total de cualquier forma sobre cualquier eje mediante la suma de la inercia rotacional de cada masa.
\begin{aligned} I &= m_1 r_1^2 + m_2 r_2^2 + \ldots \\ &= \Sigma m_i r_i^2 \end{aligned}
Figura 3: un sistema de masas rígido mostrado con dos ejes de rotación diferentes
Ejercicio 2a:
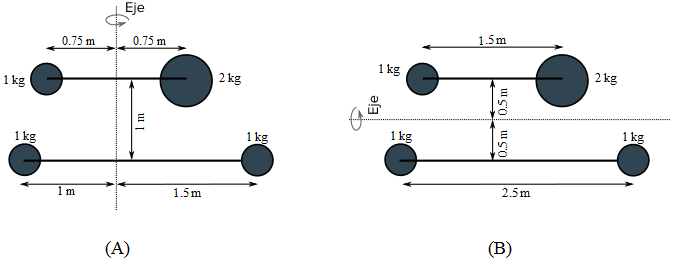
Considera el objeto que se muestra en la Figura 3. ¿Cuál es su inercia rotacional? 
[Ocultar la solución.]
Al sumar todos los términos m, r, squared para cada masa,
\begin{aligned} I &= (1~\mathrm{kg}\cdot 1^2~\mathrm{m^2}) + (1~\mathrm{kg}\cdot 1{,}5^2~\mathrm{m^2}) + (1~\mathrm{kg}\cdot 0{,}75^2~\mathrm{m^2}) + (2~\mathrm{kg}\cdot 0{,}75^2~\mathrm{m^2}) \\ &= 4{,}9375~\mathrm{kg\cdot m^2}\end{aligned}.
Ejercicio 2b:
Considera el caso alternativo de la Figura 3(b) del mismo sistema giratorio sobre un eje diferente. ¿Cuál esperarías que fuera la inercia rotacional en este caso? 
Aunque el sistema de masas es el mismo que antes, ahora rotan sobre un eje mucho más cercano. Debido a la dependencia en el cuadrado de la distancia al eje de rotación, se esperaría que la inercia rotacional sea significativamente menor.
\begin{aligned} I &= (2~\mathrm{kg}\cdot 0{,}5^2~\mathrm{m^2}) + (1~\mathrm{kg}\cdot 0{,}5^2~\mathrm{m^2}) + (1~\mathrm{kg}\cdot 0{,}5^2~\mathrm{m^2}) + (1~\mathrm{kg}\cdot 0{,}5^2~\mathrm{m^2}) \\ &= 1{,}25~\mathrm{kg\cdot m^2}\end{aligned}

¿Cómo podemos encontrar la inercia rotacional de formas complejas?

Para encontrar la inercia rotacional de figuras más complicadas generalmente es necesario usar el cálculo. Sin embargo, para muchas formas geométricas comunes, en libros de texto u otras fuentes, es posible encontrar tablas de ecuaciones que dan la inercia rotacional. Por lo general, dan el momento de inercia de una figura que gira sobre su centroide (que suele corresponder con el centro de masa de estas figuras).
Por ejemplo, la inercia rotacional de un cilindro sólido con radio r que gira al rededor de un eje central es:
I, equals, start fraction, 1, divided by, 2, end fraction, m, r, squared
y para un cilindro hueco de radios interior y exterior r, start subscript, i, end subscript y r, start subscript, o, end subscript, respectivamente,
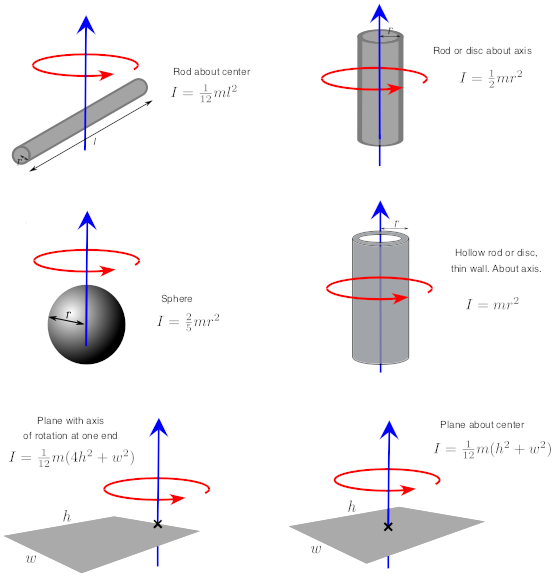
I, equals, start fraction, m, left parenthesis, r, start subscript, i, end subscript, squared, plus, r, start subscript, o, end subscript, squared, right parenthesis, divided by, 2, end fraction
Expresiones para otras figuras simples se muestran en la Figura 4.
Figura 4: las ecuaciones para la inercia rotacional de algunas formas simples bajo rotación
A menudo, las formas complejas se pueden representar como combinaciones de formas simples para las cuales existe una ecuación conocida para la inercia rotacional. Entonces podemos combinar estas inercias rotacionales para encontrar la del objeto compuesto. 
El problema con el que posiblemente nos encontremos cuando combinemos formas simples es que las ecuaciones nos dan la inercia rotacional en el centroide de la forma y esto no necesariamente corresponde al eje de rotación de la forma compuesta. Podemos tomar esto en cuenta al usar el teorema de los ejes paralelos.
El teorema de los ejes paralelos nos permite encontrar el momento de inercia de un objeto sobre un punto o siempre que conozcamos el momento de inercia de la forma alrededor de su centroide c, la masa m y la distancia d entre los puntos o y c.
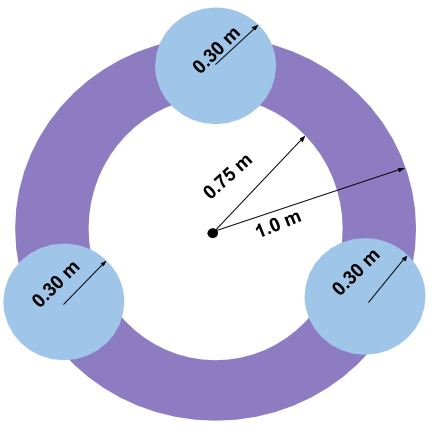
start box, I, start subscript, o, end subscript, equals, I, start subscript, c, end subscript, plus, m, d, squared, end box
Ejercicio 3:
Supón que la forma que se muestra en la Figura 5 se hace al soldar tres discos de metal de 10, space, m, m de grosor (cada uno con una masa 50, space, k, g) a un anillo de metal con masa de 100, space, k, g. Si gira alrededor de un eje central (hacia afuera de la página), ¿cuál es el momento de inercia del objeto? 
Solución
Empezamos por encontrar la inercia rotacional de los cuatro componentes por separado.
Utilizando la ecuación que determinamos previamente para un cilindro hueco, podemos encontrar la inercia rotacional I, start subscript, b, end subscript del disco grande. Este centroide de este componente ya coincide con el eje de rotación de la parte final, así que no necesitamos ningún tipo de corrección.
\begin{aligned}I_b &= \frac{1}{2} m (r_i^2 +r_o^2) \\ &= \frac{1}{2} (100~\mathrm{kg})\cdot(0{,}75^2 + 1^2)~\mathrm{m^2} \\ &\simeq 78{,}125~\mathrm{kg\cdot m^2} \end{aligned}
Usando el mismo procedimiento para los discos más pequeños, por ahora centrados en sus propios ejes de rotación:
\begin{aligned} I_s &= \frac{1}{2} m r_c^2 \\ &= \frac{1}{2}\cdot (50\cdot \mathrm{kg}) (0{,}30~\mathrm{m})^2 \\ &= 2{,}25~\mathrm{kg\cdot m^2}\end{aligned}
Como cada uno de estos tres discos rotan sobre un punto a una distancia d de sus respectivos centroides podemos utilizar el teorema de ejes paralelos para encontrar la inercia de rotación efectiva de I, start subscript, s, end subscript, prime.
d, equals, start fraction, 1, divided by, 2, end fraction, left parenthesis, 1, plus, 0, comma, 75, right parenthesis, equals, 0, comma, 875, space, m
\begin{aligned} I_s' &= I_s + md^2 \\ &= (2{,}25 ~\mathrm{kg\cdot m^2}) + (50~\mathrm{kg})\cdot (0{,}875~\mathrm{m})^2 \\ &\simeq 40{,}5~\mathrm{kg\cdot m^2}\end{aligned}
Como cada uno de los tres pequeños discos tienen el mismo radio desde el eje de rotación de la pieza, podemos tratarlos como una parte con tres veces la inercia rotacional. Por último, la inercia rotacional del objeto es:
\begin{aligned} I &\simeq 78 + 3\cdot 40{,}5 \\ &\simeq 200~\mathrm{kg\cdot m^2}\end{aligned}
Figura 5: un sistema de un disco grande y hueco y tres discos más pequeños rellenos

¿En la física, en qué otras partes aparece la inercia rotacional?

La inercia rotacional es importante en casi todos los problemas de física que involucran una masa en rotación. Se utiliza para calcular el momento angular y nos permite explicar (a través de la conservación del momento angular) cómo cambia el movimiento de rotación cuando cambia la distribución de la masa. También es necesaria para encontrar la energía que se almacena como energía cinética rotacional en un volante giratorio.

Explicación de la energía cinética rotacional