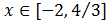Tomado de:
https://www.matesfacil.com/ESO/inecuaciones/ejercicios-resueltos-inecuaciones.html
INECUACIONES
Al resolver una inecuación o desigualdad se pretende encontrar un intervalo de valores que cumplan la relación dada, al contrario de lo que sucede en las ecuaciones en las que se encuentran valores específicos. por ejemplo si decimos x > 0 cualquier valor positivo cumple la relación por lo tanto el intervalo (0,a) será la solución.
1. Introducción
Una inecuación es una relación de desigualdad entre dos expresiones algebraicas
en las que aparece una o más incógnitas. Resolver una inecuación consiste en
encontrar todos los valores de la incógnita para los que se cumple la relación de desigualdad.
Los signos de desigualdad que se utilizan en las inecuaciones son: , , y :
-
a < b significa "a es menor estrictamente que b". Por ejemplo: 2 < 3.
-
a > b significa "a es mayor estrictamente que b". Por ejemplo: 3 > 2.
-
a ≤ b significa "a es menor o igual que b". Por ejemplo: 2 ≤ 2.
-
a ≥ b significa "a es mayor o igual que b". Por ejemplo: 3 ≥ 2.
Nota: se dice que los signos y son estrictos porque no puede darse la igualdad. Es decir, indican "menor" y "mayor", respectivamente, pero nunca "igual".
2. Solución de una inecuación
La solución de una inecuación es el valor o conjunto de valores que puede tomar
la incógnita para que se cumpla la inecuación. A diferencia de las ecuación
(cuyo signo es "="), no podemos saber de antemano el número de soluciones.
Puede darse el caso en que la solución es sólo un punto (por ejemplo, ),
un intervalo (por ejemplo, ), una unión de intervalos o que no exista
ninguna solución.
3. Tipos de inecuaciones
Inecuación lineal: cuando las expresiones de ambos lados son polinomios de
primer grado.
Ejemplo:
La solución de esta inecuación es el intervalo .
Inecuación de segundo grado: cuando las expresiones de ambos lados son
polinomios de grado menor o igual que 2.
Ejemplo:
Esta inecuación no tiene soluciones (reales) puesto que ningún número al cuadrado
es negativo.
Inecuación racional: cuando las expresiones de uno o ambos lados son un cociente
de polinomios.
Ejemplo:
La solución de esta inecuación es .
Inecuación con valor absoluto: cuando en las expresiones algebraicas hay
valores absolutos.
Ejemplo:
Esta inecuación no tiene solución porque el módulo (valor absoluto) de un número
es siempre mayor o igual que 0.
Resolvemos este tipo de inecuaciones en otra página:
4. Nota previa (para resolver inecuaciones)
La metodología de resolución es análoga a la de las ecuaciones, pero teniendo
siempre en cuenta que se trata de una desigualdad. Esto supone, por ejemplo,
cambiar el signo de desigualdad cada vez que multiplicamos o dividimos por un
negativo para mantener la relación.
Ejemplo:
Para multiplicar por un negativo, por ejemplo, -2, cambiamos la desigualdad al
resultado:
Notemos que si no la cambiamos, obtenemos una relación falsa ().
Intervalos: en los intervalos utilizaremos los símbolos "" y "" para el extremo
izquierdo y los símbolos "" y "" para el extremo derecho. Los paréntesis
indican que el extremo está incluido en el intervalo y los corchetes indican lo contrario.
Por ejemplo, el intervalo están incluido en el intervalo , pero
también en y en . Sin embargo, el intervalo no está
incluido en ni en .
Para expresar la unión de dos o más intervalos utilizamos el símbolo .
5. Inecuaciones lineales resueltas
Inecuación 1
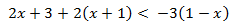
Solución
Agrupamos los monomios según su parte literal (los que tienen x y los que no)
como hacemos en las ecuaciones de primer grado, pero sin multiplicar ni dividir
toda la inecuación por un número negativo:
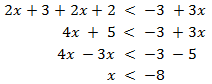
Por tanto, la solución es un intervalo:
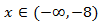
donde los paréntesis indican que los extremos del intervalo no están incluidos
(desigualdad estricta). Por ejemplo, los siguientes valores sí verifican la inecuación:
Inecuación 2
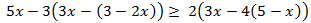
Solución
Agrupamos los monomios según su parte literal como si se tratara de una ecuación:
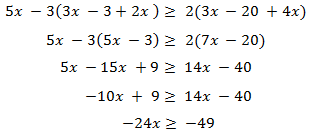
Ahora, para aislar la incógnita tenemos que dividir la inecuación por su coeficiente,
que es -24. Como este número es negativo, cambiamos el signo de desigualdad al
dividir:
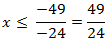
Por tanto, la solución es un intervalo:
![x pertenece al intervalo (-infinito, 49/24] Resolución de inecuaciones lineales, de segundo grado y racionales: inecuaciones simples, con fracciones (donde usaremos el mínimo común múltiplo), con paréntesis y con paréntesis anidados (unos dentro de otros). Bachiller. Bachillerato.](https://www.matesfacil.com/ESO/inecuaciones/inecuacionA2-3.png)
donde el corchete de la derecha indica que se incluye el extremo del intervalo
(es donde se cumple la igualdad).
Inecuación 3
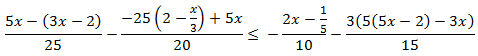
Solución
Agrupamos los monomios según su parte literal como si se tratara de una ecuación:
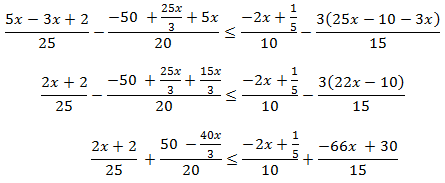
Calculamos el mínimo común múltiplo (comunes y no comunes al mayor exponente)
de los denominadores para poder sumar las fracciones:
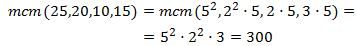
Realizamos los cambios en las fracciones y las sumamos:
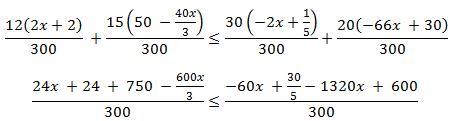
Como el denominador, 300, es positivo, podemos multiplicar toda la inecuación
por 300 para que éste desaparezca:
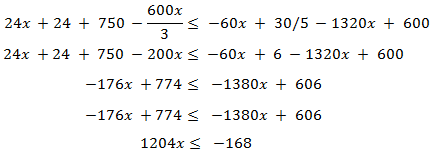
Para aislar la incógnita tenemos que dividir por su coeficiente. Como éste es positivo,
no cambia el signo de desigualdad:
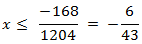
Por tanto, la solución es un intervalo:
![x pertenece al intervalo (-infinito, -6/43] Resolución de inecuaciones lineales, de segundo grado y racionales: inecuaciones simples, con fracciones (donde usaremos el mínimo común múltiplo), con paréntesis y con paréntesis anidados (unos dentro de otros). Bachiller. Bachillerato.](https://www.matesfacil.com/ESO/inecuaciones/inecuacionA3-6.png)
donde el corchete indica que también se incluye el extremo derecho.
Inecuación 4
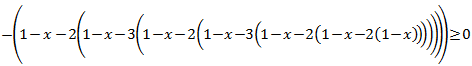
Solución
Tenemos paréntesis anidados (uno dentro de otro). No olvidemos que un signo
negativo delante de un paréntesis cambia el signo de todos los sumandos que contiene.
No existe una única forma para eliminar los paréntesis. Nosotros los eliminaremos
desde el interior al exterior:
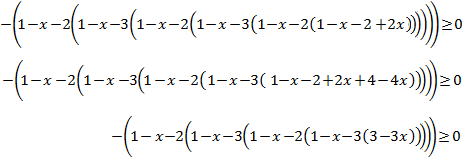
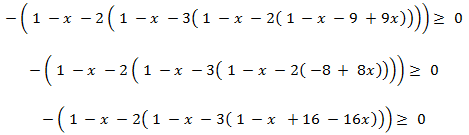
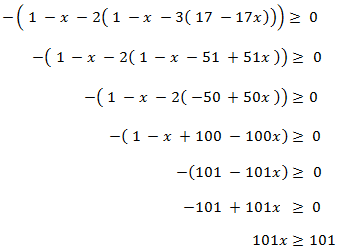
Como el coeficiente de la incógnita es positivo, no debe cambiamos la desigualdad
al aislar :
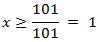
Por tanto, la solución es un intervalo:
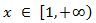
donde el corchete indica que el extremo izquierdo está incluido.
Inecuación 5
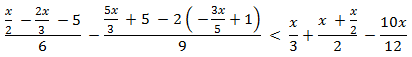
Solución
Agrupamos los monomios según su parte literal como hacemos en las ecuaciones
de primer grado. Como tenemos que sumar fracciones, multiplicaremos toda la
inecuación por el mínimo común múltiplo de los denominadores (de las fracciones
grandes).
El mínimo común múltiplo es
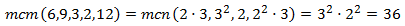
Multiplicamos:
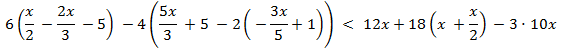
Continuamos simplificando:
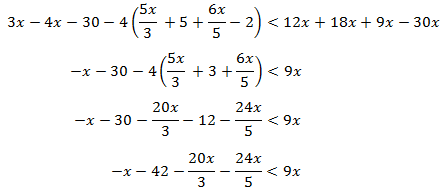
Multiplicamos por el mínimo común múltiplo de los denominadores actuales
(es decir, por 15):
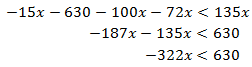
Como el coeficiente de la incógnita es negativo, cambiamos la desigualdad al
despejar :
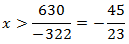
Por tanto, la solución es un intervalo:
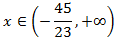
donde los paréntesis indican que no incluimos los extremos del intervalo
(la desigualdad es estricta).
6. Inecuaciones de segundo grado resueltas
Inecuación 1
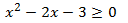
Solución
<Primero calculamos los valores para los que se cumple la igualdad. Para ello,
cambiamos la desigualdad por una igualdad. De este modo tendremos una
ecuación de segundo grado cuyas raíces determinan los extremos de los intervalos de las soluciones de la
inecuación:
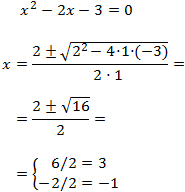
Situamos las raíces en la recta real y obtenemos 3 intervalos:
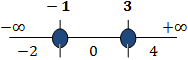
Escogemos un número al azar de cada intervalo (por ejemplo, , y )
y comprobamos si para alguno de estos valores se cumple la inecuación. No importa cuá
l escogemos puesto que el signo de la inecuación se mantiene constante en cada
intervalo.
Comprobamos:
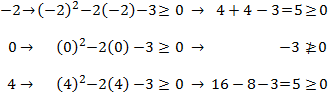
Por tanto, la inecuación se verifica en dos de los intervalos:
![x pertenece a la unión de los intervalos (-infinito, -1] y [3, + infinito) Resolución de inecuaciones lineales, de segundo grado y racionales: inecuaciones simples, con fracciones (donde usaremos el mínimo común múltiplo), con paréntesis y con paréntesis anidados (unos dentro de otros). Bachiller. Bachillerato.](https://www.matesfacil.com/ESO/inecuaciones/inecuacionB1-4.png)
donde los corchetes indican que los extremos de los intervalos están incluidos
(es en ellos donde se da la igualdad de la inecuación).
Inecuación 2
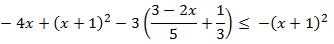
Calculamos los valores para los que se cumple la igualdad. Para ello, cambiamos
la desigualdad por una igualdad, obteniendo una ecuación de segundo grado cuyas
raíces determinan los extremos de los intervalos de las soluciones de la inecuación:
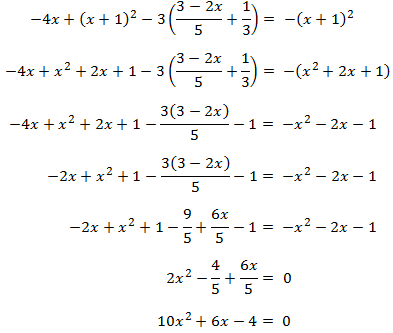
Las soluciones de la ecuación de segundo grado anterior son
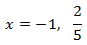
La igualdad de la inecuación se cumple para estos valores de x. Situamos las
raíces en la recta real:
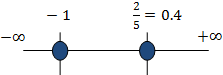
Notemos que podemos escribir la inecuación inicial como
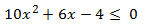
cumpliéndose la igualdad en los puntos azules (las raíces de la ecuación).
Sabemos que entre las raíces de una ecuación cuadrática el signo se mantiene
constante (si no fuera así, habría al menos un cambio de signo y, por tanto, otra raíz).
Por tanto, en los tres intervalos representados los signos se mantienen constantes.
Así que escogemos un valor cualquiera de cada uno de ellos y comprobamos
el signo. Si el signo es negativo, se cumple la inecuación y el intervalo al que
pertenece será parte de la solución de la inecuación.
Escogemos, por ejemplo, -2, 0, 1:
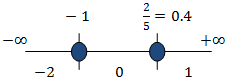
Sustituimos en la inecuación (la anterior o la inicial, es lo mismo porque son
equivalentes):
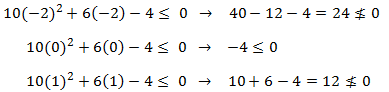
Por tanto, la solución de la ecuación es sólo un intervalo:
![x pertenece a [-1, 2/5] Resolución de inecuaciones lineales, de segundo grado y racionales: inecuaciones simples, con fracciones (donde usaremos el mínimo común múltiplo), con paréntesis y con paréntesis anidados (unos dentro de otros). Bachiller. Bachillerato.](https://www.matesfacil.com/ESO/inecuaciones/inecuacionB2-7.png)
donde los corchetes indican que los extremos del intervalo están incluidos.
Comentario: como tenemos una ecuación de segundo grado, podemos tener dos
raíces, una o ninguna. Por tanto, tendremos particiones de 3 intervalos,
2 intervalos o 1 (todos los reales). En el primer caso, si un intervalo es solución,
sus adyacentes no lo son. En el segundo, si un intervalo es solución, el otro
también. Estos hechos se deducen considerando la gráfica de la parábola y
que sus raíces son los puntos de corte con el eje de abscisas.
Inecuación 3
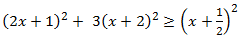
Solución
Primero calculamos los valores para los que se cumple la igualdad cambiando
la desigualdad por una igualdad y resolviendo la ecuación de segundo grado:
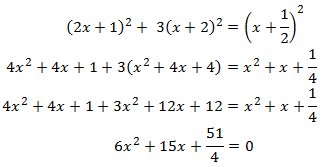
El discriminante de la ecuación es
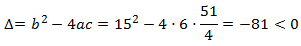
Al ser negativo, no existen soluciones reales. Esto significa que se trata de una
parábola sin cortes en el eje de las abscisas (eje OX). En otras palabras,
la parábola siempre es positiva o siempre es negativa.
Como el término principal es positivo (+6), el vértice está en la parte
inferior y, por tanto, la parábola es positiva. Podemos hacer la comprobación
dando un valor a , por ejemplo, :
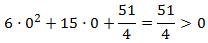
Por tanto,
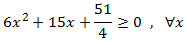
Usando la inecuación inicial,
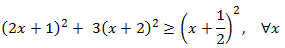
Por tanto, la solución es todos los reales:
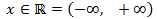
Inecuación 4
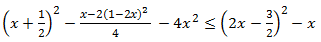
Solución
Cambiamos la desigualdad por una igualdad para obtener una ecuación de
segundo grado:
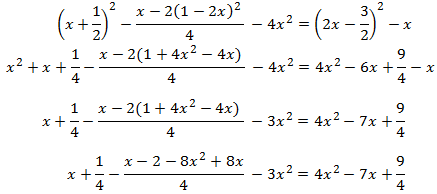
Multiplicamos por 4 para evitar los denominadores:
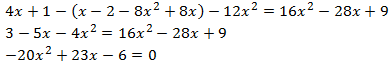
Las raíces de la ecuación son
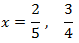
y también son los valores para los que se cumple la igualdad en la inecuación.
Luego tenemos la partición
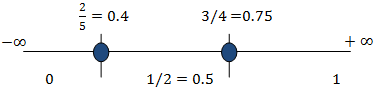
Tomamos un número de cada intervalo, por ejemplo 0, 0.5 y 1 y comprobamos
si se cumple la inecuación inicial:
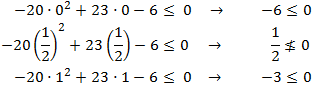
Por tanto, la solución está formada por dos intervalos:
![x pertenece a la unión de los intervalos (-infinito, 2/5] y [3/4, +infinito) Resolución de inecuaciones lineales, de segundo grado y racionales: inecuaciones simples, con fracciones (donde usaremos el mínimo común múltiplo), con paréntesis y con paréntesis anidados (unos dentro de otros). Bachiller. Bachillerato.](https://www.matesfacil.com/ESO/inecuaciones/inecuacionB4-6.png)
donde los corchetes indican que los extremos de los intervalos están incluidos.
Inecuación 5
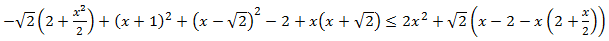
Solución
Calculamos los valores para los que se cumple la igualdad. Para ello, cambiamos
la desigualdad por una igualdad:
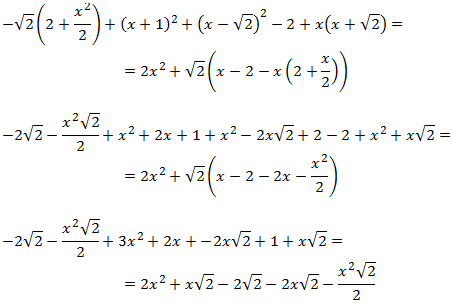
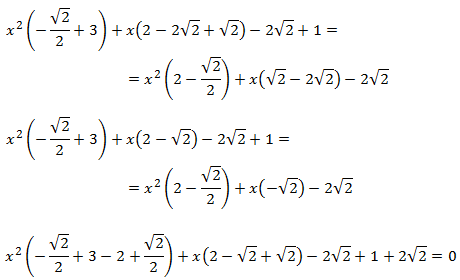
Finalmente, resolvemos la ecuación
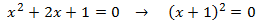
Tenemos la raíz doble . Notemos que la inecuación inicial es equivalente a
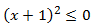
Puesto que el cuadrado de un número siempre es mayor o igual que 0, en la
inecuación sólo puede darse la igualdad. Esto ocurre cuando .
Por tanto, la única solución de la inecuación es .
7. Inecuaciones racionales resueltas
Inecuación 1
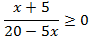
Solución
Tenemos una fracción y queremos estudiar su signo. Como estamos dividiendo,
el signo de la fracción depende de los signos del numerador y del denominador.
Cuando el numerador y el denominador tienen el mismo signo, la fracción es positiva.
Si lo tienen distinto, es negativa. Tenemos que ver las distintas posibilidades.
Primero analizamos los signos del numerador y del denominador por separado.
Numerador:
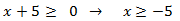
Denominador:
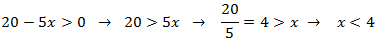
La segunda desigualdad es estricta (sin el igual) ya que el denominador no puede ser 0.
Representamos los valores en dos rectas indicando el signo en cada intervalo:
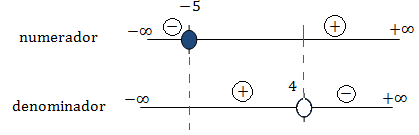
Hemos representado una recta encima de otra porque ahora tenemos que trabajar
con ambas.
El único intervalo para el que el numerador y el denominador tienen el mismo signo
(y por tanto, la solución de la inecuación) es:
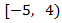
Siendo ambos positivos en el intervalo. El corchete indica que se incluye el extremo
del intervalo ya que en él es donde se cumple la igualdad de la inecuación.
Inecuación 2
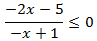
Solución
Primero analizamos los signos del numerador y del denominador por separado.
Como queremos que la fracción sea negativa (o cero), el signo del numerador
y del denominador han de ser distintos (o el numerador 0).
Numerador:
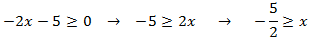
Denominador:
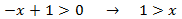
Notemos que hemos escrito desigualdad estricta para el denominador porque éste
no puede ser 0.
Representamos los valores en dos rectas indicando el signo en cada intervalo:
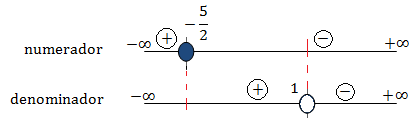
Hemos representado una recta encima de otra porque ahora tenemos que trabajar
con ambas.
El único intervalo para el que el numerador y el denominador tienen signos distintos
(y por tanto, la solución de la inecuación) es:
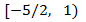
El corchete indica que se incluye el extremo del intervalo ya que en él es donde se
cumple la igualdad de la inecuación.
Inecuación 3
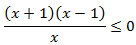
Solución
Para que la fracción sea negativa (o cero), el signo del numerador y del denominador
han de ser distintos (o el numerador 0).
Numerador: es una ecuación de segundo grado, pero por la forma en la que
está escrita (factorizada) sabemos que las raíces son 1 y -1. Estudiamos el signo
en los tres intervalos:
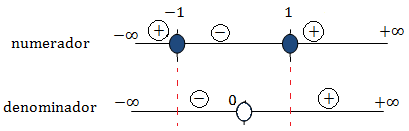
No olvidemos que no puede valer 0 en el denominador (denominador nulo).
Mirando las rectas obtenemos los intervalos donde los signos son distintos:
![unión de los intervalos (-infinito, -1] y (0,1] Resolución de inecuaciones lineales, de segundo grado y racionales: inecuaciones simples, con fracciones (donde usaremos el mínimo común múltiplo), con paréntesis y con paréntesis anidados (unos dentro de otros). Bachiller. Bachillerato.](https://www.matesfacil.com/ESO/inecuaciones/inecuacionC3-2.png)
Donde los corchetes indican que los extremos del intervalo están incluidos.
Inecuación 4
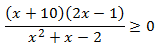
Solución
Como la fracción tiene que ser positiva, queremos que el signo del numerador
y el del denominador sean el mismo.
Tanto numerador como denominador son polinomios de segundo grado.
Numerador: las raíces son -10 y 1/2
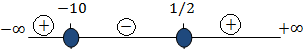
Denominador: calculamos las raíces
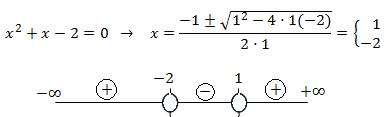
Los intervalos donde coinciden los signos (y por tanto, la solución de la inecuación) son
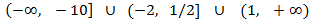
donde los corchetes indican que los extremos de los intervalos están incluidos
(-2 y 1 no se incluyen porque son los valores para los que el denominador se anula).
Inecuación 5
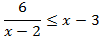
Solución
Vamos a operar en la inecuación para obtener una expresión como las anteriores
(fracción menor o igual que 0).
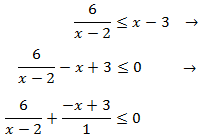
Para poder sumar las fracciones, multiplicamos y dividimos la fracción de la
derecha por el denominador de la de la izquierda:
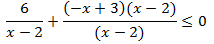
Ahora ya podemos sumarlas:
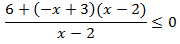
Operamos:
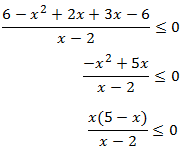
Estudiamos los signos en los diferentes intervalos:
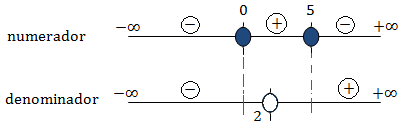
Los intervalos donde no coinciden los intervalos son (y por tanto, la solución de
la inecuación)

Introducción
El valor absoluto de un número a, representado como |a|, es su valor numérico (con signo positivo).
Por ejemplo,
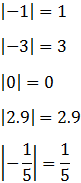
Notemos que:
-
si el número es positivo, su valor absoluto es el propio número;
-
si el número es negativo, su valor absoluto es su opuesto (número con signo opuesto, es decir, con signo positivo);
-
si el número es 0, su valor absoluto es 0, aunque 0 no es ni positivo ni negativo.
Definición de la función Valor Absoluto
Propiedades del Valor Absoluto
Inecuaciones Resueltas
Antes de empezar, diremos que en todos los problemas usaremos la cuarta propiedad del apartado "Propiedades del Valor Absoluto".
Inecuación 1
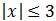
Escribimos la inecuación como
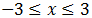
Por tanto, la solución es
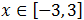
Inecuación 2
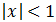
Escribimos la inecuación como
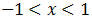
Por tanto, la solución es
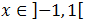
O bien, con la notación de paréntesis,
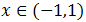
En cualquier caso, los extremos del intervalo son abiertos (porque la desigualdad es estricta).
Inecuación 3
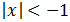
Esta inecuación no tiene solución ya que el valor absoluto de un número siempre mayor o igual que 0.
Inecuación 4
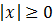
La solución es todos los reales:
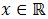
ya que el valor absoluto siempre es mayor o igual que 0.
Inecuación 5
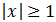
Tiene que cumplirse una de las siguientes relaciones:
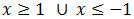
Por tanto, la solución es
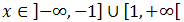
Inecuación 6
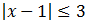
Podemos escribir la inecuación como
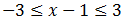
Tenemos que resolver las dos inecuaciones.
Podemos hacerlo al mismo tiempo:
Sumamos 1:
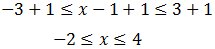
O bien, separar ambas inecuaciones y resolverlas por separado:
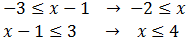
De ambas formas obtenemos la misma solución:
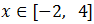
Inecuación 7
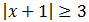
Tenemos las dos inecuaciones:

Las resolvemos:
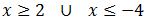
Por tanto, la solución es
Inecuación 8
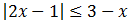
Escribimos la inecuacón como
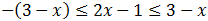
Por tanto,
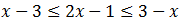
Resolvemos cada inecuación:
Por un lado:
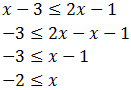
Por otro lado:
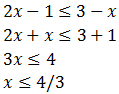
Inecuación 9
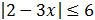
Escribimos la inecuación como
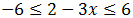
Por un lado:
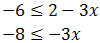
Tenemos que estar alerta en el último paso ya que el coeficiente de la incógnita es negativo. Al dividir por -3 tenemos que cambiar el signo de la inecuación:
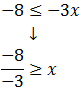
Por otro lado:
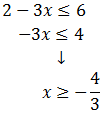
Por tanto, la solución es
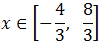
Inecuación 10
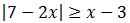
Debe cumplirse alguna de los dos inecuaciones:
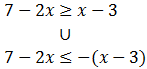
Resolvemos la primera:
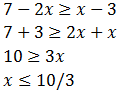
Resolvemos la segunda:
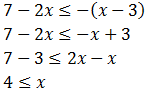
Por tanto, la solución es:
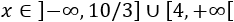
Inecuación 11
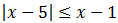
Escribimos la inecuación como:
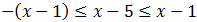
Vamos a trabajar primero con las dos inecuaciones al mismo tiempo:
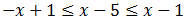
Sumamos 5:
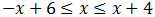
Sumamos x:
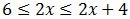
Ahora tenemos que separarlas para obtener la solución:
Por un lado:
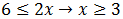
Por otro:
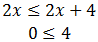
En esta segunda inecuación hemos obtenido una relación que siempre se cumple. Luego no nos aporta restricciones a la solución.
Por tanto, la solución es
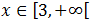
Inecuación 12: dificultad alta
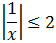
Tenemos las dos inecuaciones:
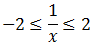
Resolvemos la primera:
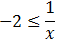
No podemos multiplicar por x porque no sabemos si es positiva o negativa.
Supongamos que x es positiva ( x > 0): ahora sí podemos multiplicar por x :
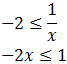
Por tanto, cambiando la desigualdad al dividir por el negativo -2, tenemos
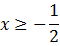
Pero hemos dicho que x > 0, luego al unir ambas condiciones tenemos que

(ya que es la más restrictiva).
Supongamos ahora que x es negativa: x < 0:
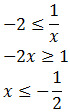
Por tanto, la solución a esta primera inecuación es
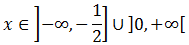
Resolvemos la segunda inecuación procediendo del mismo modo:
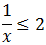
Si x es positiva:
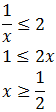
Si x es negativa:
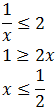
Por tanto, la solución a la segunda inecuación es:
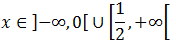
Las soluciones de las dos inecuaciones son:
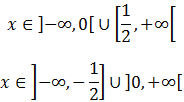
Y tienen que cumplirse ambas.
Por tanto, la solución es
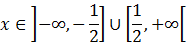
Inecuación 13: dificultad muy alta
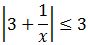
Tenemos las dos inecuaciones:
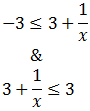
Resolvemos la primera:
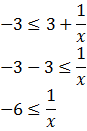
Ahora no podemos multiplicar la inecuación por x porque ésta podría ser negativa y, entonces, habría que cambiar el signo de desigualdad.
Supongamos que x es positiva. Ahora podemos multiplicar:
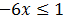
Como el coeficiente de la x es negativo, cambiamos el signo de desigualdad al dividir por -6:
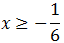
Pero, además, sabemos que x tiene que ser positiva:
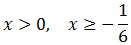
Por tanto, tenemos que ha de ser

Ahora suponemos que x es negativa. Al multiplicar por x tenemos que cambiar el signo de desigualdad:
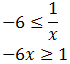
Por tanto,
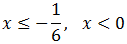
Luego
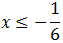
Resolvemos la segunda inecuación procediendo de forma similar:
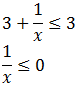
Si x es positiva:
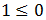
Lo cual es falso. Por tanto, x no puede ser positiva.
Si x es negativa:
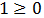
Lo cual siempre se cumple (no aporta restricciones a la solución).
Las soluciones que hemos obtenido son, de la primera inecuación
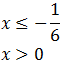
Y de la segunda: que x no puede ser positiva.
Por tanto, como deben cumplirse ambas inecuaciones, la solución es
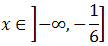
14. Resolver la ecuación
-
Si x 2 - 4> = 0, ó x 2 >= 4, entonces | x 2 - 4 | = x 2 - 4 y la ecuación dada se convierte en
x 2 - 4 = x + 2
-
Añadir - (x + 2) a
ambos lados
x 2 - 4 - (x + 2) = 0
-
Factor de la expresión
a la izquierda
(x - 2) (x + 2) - (x + 2) = 0
(x + 2) (x - 2 -1) = 0
(x + 2) (x - 3) = 0
-
Usando el teorema de
los factores, podemos escribir dos ecuaciones simples
x + 2 = 0
o
x - 3 = 0
-
Resolver las
ecuaciones anteriores para x para encontrar dos valores de x que hacen que el lado izquierdo de la ecuación igual a cero.
x = -2 y x = 3.
-
Ambos valores
satisfacen la condición x 2> = 4 y soluciones a la ecuación dada.
x = -2 y x = 3.
-
Si x 2 - 4 <0, o x 2 <4, entonces | x 2 - 4 | = - (x 2 - 4) y la ecuación que se hace.
- (x 2 - 4) = x + 2
- (x 2 - 4) - (x + 2) = 0
-
Factor de la expresión
a la izquierda.
- (x - 2) (x + 2) - (x + 2) = 0
(x - 2) (x + 2) + (x + 2) = 0
(x - 2) (x + 2) + (x + 2) = 0
(x + 2) (x - 2 + 1) = 0
(x + 2) (x - 1) = 0
-
Dos valores que el
lado izquierdo de la ecuación anterior es igual a cero
x = -2 y x = 1.
- Sólo x = 1 satisface la condición x 2 < 4
Luego la solución es