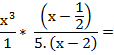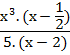Esta clase fue tomada de: https://matematicaylisto.webcindario.com/polinomios/expralge/racionals.htm
SOBRE SIMPLIFICACIÓN DE EXPRESIONES ALGEBRAICAS RACIONALES
¿Cómo se simplifica en una fracción "con polinomios arriba y abajo"?
Como ya comenté antes, el conjunto de los polinomios "se comporta" igual que el conjunto de los Números Enteros (![]() ). Eso quiere decir que, "lo mismo que se hace con
los números enteros se puede hacer con los polinomios". Veamos entonces lo que ya se sabe que podemos hacer con los números enteros para comparar ambos temas. Supongamos que tenemos la siguiente
fracción con números enteros multiplicando en el numerador y en el denominador:
). Eso quiere decir que, "lo mismo que se hace con
los números enteros se puede hacer con los polinomios". Veamos entonces lo que ya se sabe que podemos hacer con los números enteros para comparar ambos temas. Supongamos que tenemos la siguiente
fracción con números enteros multiplicando en el numerador y en el denominador:
![]()
Sabemos que se pueden simplificar los números que se encuentren repetidos, "uno de arriba con uno de abajo" (no lo sabía ¿por qué se puede?). Así, tachamos "el 2 con el 2", "el 3 con el 3"
y el "5 con el 5":
![]() 7 (Lo único que no se simplificó fue el 7) (¿por qué quedó 7?)
7 (Lo único que no se simplificó fue el 7) (¿por qué quedó 7?)
Con los polinomios vamos a hacer lo mismo: Si "arriba y abajo" de la fracción hay un mismo polinomio multiplicando o solo (¿por qué cuando está solo?: ver EJEMPLO 3), puedo
simplificarlos. Es decir: cancelar uno con uno.
Nota: esta simplificación de polinomios no vale para cualquier valor de la x (o la letra que tenga el polinomio). Esta
simplificación no vale para valores de x que hagan que el polinomio dé cero, al igual que no valdría simplificar el número cero en una fracción numérica (¿por qué?). En Nivel Medio puede que no te pidan que aclares esto, pero antes de simplificar
habría que aclararlo (cómo sería eso).
Por ejemplo:
![]()
Aquí puedo "tachar" el (x + 1) que está multiplicando "arriba" con el (x + 1) que está multiplicando "abajo". Lo mismo con el (x - 5), y también con el
(x2 + 1). Así:
![]()
Luego, solo quedan sin tachar el (x - 3) arriba y el (x + 5). El resultado es:
![]()
Por supuesto que los resultados pueden tener distinta forma, dependiendo si se simplifica todo arriba, todo abajo, si hay números multiplicando también, etc. Todas
esas posibilidades se contemplan en los diferentes EJEMPLOS que expuse arriba, y son explicadas en cada apartado.
Puede observarse también que en este ejemplo todos los polinomios que puse son "binomios", y casi todos de grado 1. Elegí ese tipo de polinomios porque es con lo
que nos vamos a encontrar la mayoría de las veces en este tema. Pero también se pueden simplificar polinomios de grado más alto, o "letras solas" que estén multiplicando (monomios), o números que
queden multiplicando (polinomios de grado 0). Esas variantes se ven y explican en los EJEMPLOS que dí arriba en esta página.
Ahora bien: los ejercicios que nos dan para resolver no tienen en un principio binomios repetidos multiplicando arriba y abajo como en el ejemplo anterior. Son más
bien así:
![]()
Pero si factorizamos los polinomios en el numerador y en el denominador (los que se puedan factorizar), llegaremos a la forma que tiene el ejemplo que
dí:
![]()
Ahora sí tenemos "polinomios multiplicando arriba y abajo". Y es porque al factorizar estamos transformando en multiplicación. Y justamente, el que queden
multiplicando, es lo que nos permite simplificar los "polinomios repetidos", tal como decía que hacemos con los número enteros:
![]()
Hagamos una analogía entre esta situación (que los polinomios no están factorizados en un principio) y la simplificación de las fracciones numéricas. Si tenemos que
simplificar una fracción con números compuestos (¿qué son los números compuestos?), los podemos descomponer (¡que también se le llama "factorizar"!), y luego "tachar" los factores repetidos. Por
ejemplo:
![]()
Descomponer los números en sus factores primos sería lo análogo a factorizar los polinomios:
24 = 2.2.2.3
20 = 2.2.5
La fracción entonces queda así:
![]()
Donde podemos simplificar así:
![]()
Como en general no hacemos esto para simplificar fracciones numéricas (sino que dividimos el numerador y el denominador por un mismo número), la analogía puede no
resultarnos tan evidente.
Los polinomios que factorizamos ¡también son compuestos!, y los estamos factorizando "en sus factores primos", tal como a los números enteros (¿primos y compuestos?).
¿Por qué en una fracción se puede simplificar "algo que está multiplicando arriba con algo que está multiplicando abajo?
Ya hablé de esto en otro apartado (Ver aquí), pero allí expliqué más que nada el "cómo" simplificar. Ahora voy a tratar de justificar un poco más a fondo el "por
qué". Usemos el siguiente ejemplo
![]()
Esa fracción equivale a la siguiente operación:
(2.3.5):(2.7)
ya que la línea de fracción representa división. En (2.3.5), estamos multiplicando por 2 a (3.5)
(la multiplicación "es
asociativa"). Luego, al dividir por (2.7), estamos dividiendo por 2 y dividiendo por 7, ya que hay una propiedad de los
números enteros que dice algo así:
a:(b.c) = (a:b):c
Es decir, dividir por una multiplicación es lo mismo que dividir por uno de los factores, y al resultado dividirlo por el otro. No voy a ahondar en
esto: simplemente lo estoy usando para justificar que en el ejemplo estoy multiplicando por 2 y luego dividiendo por 2. Y si multiplico y divido por el mismo número (distinto de
cero, aclaremos), es lo mismo que si no hiciera nada: como son operaciones opuestas, vuelvo al resultado inicial. Si vuelvo al resultado inicial, entonces puedo no hacer nada, y por eso puedo
"tachar" los dos números y no hacer nada. Eso es simplificar. Tachar algo porque no hace falta hacer nada con ello, ya que si lo hiciera no cambiaría el resultado.
En el caso particular en que haya un solo número arriba o abajo, podemos pensar igual que ese número está multiplicando: está multiplicando a "1". Por
ejemplo:
![]()
¿Por qué es 7 el resultado primer ejemplo que dí?
En el ejemplo que dí arriba:
![]()
simplifiqué todo menos el 7. Al simplificar, cada número que tacho queda en 1. Porque recordemos que otra forma de pensar la simplificación (la más común) es:
"divido el de arriba y el de abajo por el mismo número". Si a 2 lo divido por 2 me queda 1. Lo mismo con el 2 de abajo. Y lo mismo con los dos "3" y los dos "5". Se suele poner así:
1 1 1
![]()
1 1 1
Entonces, arriba me queda: 1.1.7.1 = 7. Y abajo, 1.1.1 = 1. El resultado es la fracción 7/1, que es igual a 7.
¿Se puede simplificar cualquier número?
No, el cero no se puede simplificar de esta manera. En un principio, por el hecho de que "no se puede dividir por cero" o "la división por cero no está permitida",
nunca en una fracción numérica voy a encontrar un ejercicio así:
![]()
Porque es esa fracción el cero está dividiendo, y eso no se puede. En cuanto a simplificar, habíamos dicho que se podía porque "multiplicar por un número y luego
dividir por ese mismo número es lo mismo que no hacer nada, ya que el resultado no cambia". Eso pasa con todos los números, con excepción del cero. Porque por cero no se puede dividir. Por
ejemplo:
(7.2):2 = 7
Puedo simplificar el 2 con el 2, porque el resultado es 7; entonces no hace falta multiplicar por 2 y dividir por 2, porque es lo mismo no hacerlo: dá el mismo
resultado si no haga nada. En cambio:
(7.0):0 no es igual a 7. Ni siquiera se puede calcular, porque no se puede dividir por cero. Entonces no puedo simplificar el cero; ya que si simplifico, el
resultado sería 7; pero eso no es verdad: no dá 7 esa cuenta, esa cuenta no se puede hacer: no tiene resultado.
Por eso, cuando simplifico polinomios, tengo que aclarar que la simplificación vale solamente para todos los valores de la x (o la letra del polinomio) que no hagan
que el polinomio dé cero. A ver con un ejemplo si se entiende mejor:
![]()
Allí se pueden simplificar los (x - 3), siempre que (x - 3) no valga cero. Por lo que dijimos antes. ¿Y cuándo (x - 3) vale cero?: cuando la x vale 3. Porque (3 -
3) = 0. Entonces, debo aclarar que vale simplificación para todo valor de x desigual a 3:
![]()
En el ejemplo que dí más arriba:
![]()
La simplificación vale para todo x desigual a -1 y 5:
![]()
¿Por qué?
a) Porque puedo simplificar a los (x + 1) siempre que no valgan cero. Y (x + 1) vale cero cuando x = -1. Ya que (-1 + 1) = 0. ¿Y si no me doy cuenta "mentalmente"
cuál es el valor de x que hace que dé cero? Entonces planteo la siguiente ecuación y la resuelvo:
x + 1 = 0
x = 0 - 1
x = -1
Así puedo encontrar el número si no me doy cuenta.
b) Y puedo simplificar a los (x - 5) siempre que no valgan cero. Y (x - 5) vale cero cuando
x = 5. Ya que (5 - 5) = 0. Para averiguar ese número podría haber hecho:
x - 5 = 0
x = 0 + 5
x = 5
c) Y puedo simplificar a los (x2 + 1) siempre que no valgan cero. Pero resulta que (x2 + 1) no puede valer cero: no hay ningún valor
de x que haga que (x2 + 1) sea igual a cero. Y para averiguar eso podría haber hecho:
x2 + 1 = 0
x2 = 0 - 1
x2 = -1
Y esa ecuación no tiene solución, ya que no hay ningún número (dentro de los conjuntos con los que trabajamos: Enteros, Racionales, Reales) que elevado al cuadrado
dé como resultado -1. (O "no se puede calcular la raíz cuadrada de -1". La calculadora dá "error")
Entonces, el (x2 + 1) lo podemos simplificar siempre, para cualquier valor de x. No hace falta aclarar nada respecto a esa simplificación: vale para
todos los valores de x.
De los puntos a), b) y c), concluimos que la simplificación de los polinomios repetidos en ese ejercicio vale para todo número distinto de -1 y 5.
Propiedad asociativa de la multiplicación:
(a.b).c = a.(b.c) = a.b.c
Es decir, si tengo el producto de varios factores, puedo "asociarlos" de distinta manera, es decir: hacer las multiplicaciones en distinto orden, pero el resultado
al que llego es el mismo. Por ejemplo:
(2.3).5 = 6.5 = 30
2.(3.5) = 2.15 = 30
2.3.5 = 30
SIMPLIFICACION DE EXPRESIONES ALGEBRAICAS RACIONALES / EJERCICIOS RESUELTOS |
|
|
EJEMPLO 1: |
|
|
|
|
SOBRE MULTIPLICACIÓN DE EXPRESIONES ALGEBRAICAS RACIONALES
SOBRE MULTIPLICACIÓN DE EXPRESIONES ALGEBRAICAS RACIONALES
¿Cómo se multiplican las fracciones "con polinomios arriba y/o abajo"?
Hay que multiplicar "lo de arriba por lo de arriba" y "lo de abajo por lo de abajo", igual que
como lo hacíamos con las fracciones numéricas. Recordemos con un ejemplo:
![]()
En general sería:
![]()
Pero también, si podíamos, nos convenía simplificar antes de multiplicar. Y se podía
simplificar "alguno de arriba con alguno de abajo". Por ejemplo:
3
![]()
1
Allí pude simplificar el 6 que estaba "arriba" con el 2 que estaba "abajo". Y luego
multipliqué.
Con las fracciones con polinomios hay que hacer lo mismo. Pero en este tema casi siempre
encontraremos polinomios que se pueden factorizar, entonces conviene hacerlo para encontrar más "cosas" (factores) para simplificar, como ya vimos en la parte de SIMPLIFICACIÓN DE EXPRESIONES ALGEBRAICAS.
Los pasos serían entonces, en la mayoría de los ejercicios, los siguientes:
1) Factorizar totalmente todos los polinomios que se puedan
2) Simplificar todo lo que se pueda, siempre "uno de arriba con uno de abajo" de cualquier
fracción. (más sobre simplificar en SIMPLIFICACIÓN)
3) Multiplicar los polinomios que quedaron "arriba". Y multiplicar los que quedaron "abajo".
El resultado es una fracción cuyo numerador es igual a la multiplicación de "los de arriba", y cuyo denominador es igual a la multiplicación de "los de abajo". Tal como en se hace con la
multiplicación de las fracciones numéricas.
EJEMPLOS:
![]() En este ejemplo no hay
nada para factorizar
En este ejemplo no hay
nada para factorizar
1
![]() Se puede simpliflicar
el (x + 3) de arriba con el de abajo
Se puede simpliflicar
el (x + 3) de arriba con el de abajo
1
![]() Luego se multiplican los numeradores entre
sí, y lo mismo con los denominadores
Luego se multiplican los numeradores entre
sí, y lo mismo con los denominadores
![]() Se puede factorizar el polinomio x2 - 4
Se puede factorizar el polinomio x2 - 4
![]() Luego de factorizar vemos que el
polinomio (x - 2) se repite
Luego de factorizar vemos que el
polinomio (x - 2) se repite
1
![]() Simplifico los (x - 2), ya uno está
"arriba" y el otro "abajo"
Simplifico los (x - 2), ya uno está
"arriba" y el otro "abajo"
![]() Luego
de multiplicar numeradores entre sí, y denominadores entre sí.
Luego
de multiplicar numeradores entre sí, y denominadores entre sí.
|
EJEMPLO 1: |
|
|
EJEMPLO 3: |
|
SOBRE DIVISIÓN DE EXPRESIONES ALGEBRAICAS RACIONALES
¿Cómo se dividen las fracciones "con polinomios arriba y/o abajo"?
Recordemos que para dividir las fracciones numéricas, podíamos "transformar en multiplicación
dando vuelta la segunda fracción". Por ejemplo, hacíamos así:
![]()
Bueno, para dividir las Expresiones Algebraicas Racionales, se suele usar ese mismo
procedimiento. Por ejemplo:
![]()
Una vez transformada la operación en una multiplicación, se aplica todo lo que ya vió para
multiplicación: simplificar y multiplicar numeradores entre sí y denominadores entre sí.
Así que, la diferencia con la multiplicación es sólo un paso donde se invierte la segunda
fracción. Una vez que se aprendió a multiplicar, ya se sabe todo lo necesario para dividir.
(Todo sobre multiplicación de expresiones algebraicas racionales)
¿Y no se podría hacer con el otro método para dividir fracciones?
Sí, por supuesto. Recordemos que el otro método para dividir fracciones numéricas era
"multiplicar cruzado", así:
![]()
Es decir: se multiplica el numerador de la primera por el denominador de la segunda, y el
denominador de la primera por el numerador de la segunda. El resultado es la fracción formada por ambos resultados.
Pero en este tema de las fracciones con polinomios, casi siempre tendremos que simplificar
antes de multiplicar. Entonces, conviene recordar cómo se puede simplificar en una división: "numerador con numerador o denominador con denominador" (lo contrario de lo que se hace en la
multiplicación de fracciones). Lo muestro en un ejemplo numérico:
1 4
![]()
Y acá muestro cómo sería con el EJEMPLO de fracciones con polinomios:
![]()
![]() no lo transformo en multiplicación, no invierto la segunda fracción
no lo transformo en multiplicación, no invierto la segunda fracción
![]() simplifico como se debe en una división
simplifico como se debe en una división
![]()
![]() aplico la regla para la división de fracciones: producto cruzado
aplico la regla para la división de fracciones: producto cruzado
![]() 3.(x - 2)
3.(x - 2)
¿Qué es la "fracción inversa" de una fracción?
Podemos decir que es la fracción "al revés" de ella. Por ejemplo, la fracción inversa de 2/5 es 5/2. La fracción inversa de 4/7 es 7/4.
2/5 y 5/2 son fracciones inversas entre sí
4/7 y 7/4 son fracciones inversas entre sí
Es decir, es la que tiene en el numerador el denominador de la otra; y tiene en el denominador, el numerador de la otra: "Tiene los números cambiados de lugar", "el de arriba lo tiene abajo, y el
de abajo lo tiene arriba".
Y cuando multiplico dos fracciones inversas entre sí, el resultado es 1:
2/5 x 5/2 = 1
4/7 x 7/4 = 1
A una fracción que es inversa de otra se le llama "el inverso multiplicativo". El "inverso multiplicativo" de un número real es otro número tal que, multiplicado por el primero, dé como resultado
"1". Todos los números reales tienen inverso multiplicativo, con excepción del cero.
|
EJEMPLO: |
|
|
EXPLICACIÓN: |
|
SOBRE SUMA Y RESTA DE EXPRESIONES ALGEBRAICAS
RACIONALES
¿Cómo se suman y/o restan las fracciones "con polinomios arriba y/o abajo"?
Igual que se suman y/o restan las fracciones numéricas: se busca un denominador común, y luego se sigue el procedimiento que ya es conocido para sumar fracciones numéricas. Recordémoslo con un
ejemplo:
![]()
1) Se busca un denominador común, que debe ser el llamado Mínimo Común Múltiplo (m.c.m.) entre los denominadores. El m.c.m. de 4 y 6 es 12 (¿cómo se calcula el m.c.m. entre números?). Porque 12 es divisible por 4 y por 6, y es el menor
número que cumple con eso. A veces, ese m.c.m. es el producto de los dos denominadores, por ejemplo si ellos fueran 3 y 7, el m.c.m es 3.7 = 21.
2) Luego se divide a éste por los denominadores de cada fracción, y se multiplica el resultado por el numerador de la fracción correspondiente:
12:4 = 3 y se multiplica por el numerador: 5.3 = 15
12:6 = 2 y se multiplica por el numerador: 1.2 = 2
3) Finalmente se hace la operación indicada en el numerador: suma o resta. Y si se puede, simplificamos la fracción que nos dá como resultado.
Con las fracciones polinómicas tenemos que hacer lo mismo. Voy a mostrar, con un ejemplo, cómo es en general el procedimiento. Pero para entender cómo hacer cualquier ejercicio será necesario ver
varios ejemplos de los que presenté en esta página y leer sus respectivas explicaciones.
![]()
1) El denominador común entre (x + 2) y (x - 3) es el m.c.m. entre esos polinomios, que en este caso es el producto de ambos: (x + 2).(x - 3). Ya en otro apartado explicaré en detalle cómo
calcular el m.c.m. entre polinomios (ver
aquí).
2) Luego se divide el denominador común por el numerador de cada fracción, y se multiplica el resultado por el numerador de la fracción correspondiente:
En la primera fracción:
(x + 2).(x - 3) dividido (x + 2) es igual a (x - 3). Y se multiplica el resultado por el numerador: x.(x - 3).
(Luego explicaré cómo se hacen esas divisiones: Ver aquí. Pero si se dan cuenta pueden ir observando que se "cancela" el polinomio por el cual se está
dividiendo, y queda el otro).
(x + 2).(x - 3) dividido (x - 3) es igual a (x + 2). Y se multiplica el resultado por el numerador: 2.(x + 2).
![]() Y luego se efectúan las multiplicaciones, que a veces requieren de
aplicar la propiedad distributiva:
Y luego se efectúan las multiplicaciones, que a veces requieren de
aplicar la propiedad distributiva:
![]() 3) Luego se hace la operación indicada en el numerador. En este
ejemplo es una suma, así que hay que sumar los dos polinomios que quedaron: (x2 - 3x) + (2x + 4). Recordemos que en la suma de polinomios se suman los términos de igual
grado.
3) Luego se hace la operación indicada en el numerador. En este
ejemplo es una suma, así que hay que sumar los dos polinomios que quedaron: (x2 - 3x) + (2x + 4). Recordemos que en la suma de polinomios se suman los términos de igual
grado.
En este tema ya no es necesario interpretar que en el numerador hay una suma o resta de polinomios: simplemente se pueden quitar los paréntesis y "juntar" los términos de igual grado, para llegar
a la mínima expresión del polinomio (es decir, que sólo haya un término de cada grado). En este ejemplo "junté" el -3x con el 2x, para que quede un sólo término de grado 1: -x
![]() Luego, si en el numerador se pudiera aplicar un Caso de Factoreo, se
hace. Porque en la factorización podría aparecer polinomio que se podría simplificar con uno del denominador. En este ejemplo en particular no se puede factorizar a x2 - x +
4 por ningún Caso de Factoreo.
Luego, si en el numerador se pudiera aplicar un Caso de Factoreo, se
hace. Porque en la factorización podría aparecer polinomio que se podría simplificar con uno del denominador. En este ejemplo en particular no se puede factorizar a x2 - x +
4 por ningún Caso de Factoreo.
En los 14 EJEMPLOS que presenté en esta página, se puede ver la variedad de situaciones que se presentan a la hora de buscar denominador común. En los enlaces de EXPLICACIÓN DEL EJEMPLO se puede
encontrar una detallada descripción de todos los pasos a seguir en cada ejercicio, cómo se halló el denominador común o m.c.m., etc.
¿Cómo se determina el denominador común entre dos fracciones con polinomios?
El denominador común a usar en una suma o resta de fracciones es siempre el mínimo común múltiplo (m.c.m.) entre todos los denominadores de las fracciones que se están sumando y restando. Como ya
dije antes, en otra sección explicaré cómo hallar el m.c.m. entre polinomios (ver aquí). Pero por ahora, podemos ver algunos casos particulares en donde hallar el
denominador común es muy fácil, y no requiere saber calcular el m.c.m. entre polinomios.
1) Cuando los denominadores de las fracciones son iguales: Igual que en la suma de las fracciones numéricas, si los denominadores son iguales, el denominador común es ése denominador. Por
ejemplo:
![]()
En el EJEMPLO 1 presentado en esta página se puede ver esta situación en
una suma de fracciones con polinomios
2) Cuando alguno de los términos no tiene denominador: El denominador común es el el único denominador que hay. Por ejemplo:
![]()
En el EJEMPLO 12 presentado en esta página se puede ver esta situación en
una suma de fracciones con polinomios
3) Cuando los denominadores son polinomios distintos y que no se pueden factorizar: El denominador común es el producto de ambos polinomios. Por ejemplo:
![]()
![]() 4) Cuando los denominadores tienen un solo término, y es la misma letra aunque
con distinto exponente: El denominador común es esa letra con el mayor exponente:
4) Cuando los denominadores tienen un solo término, y es la misma letra aunque
con distinto exponente: El denominador común es esa letra con el mayor exponente:
![]()
|
EJEMPLO 1: (Suma de fracciones
con igual denominador) |
||||
|
EJEMPLO 3: (Con denominadores distintos)
|
||||
SOBRE OPERACIONES COMBINADAS CON EXPRESIONES ALGEBRAICAS
RACIONALES
¿Cómo se resuelven los ejercicios combinados de expresiones algebraicas?
Como los ejercicios combinados de conjuntos numéricos: Se separa en términos, los paréntesis,
corchetes y llaves están para indicar que primero hay que resolver lo que está dentro de ellos, las operaciones tienen la misma prioridad: Primero las multiplicaciones y divisiones, luego las
sumas y restas, etc. Es decir que se puede ver a cada fracción con polinomios como si fuera una fracción numérica en un ejercicio combinado con fracciones numéricas, y trabajar con ellas de la
misma forma.
EJEMPLO 1:
![]()
![]()
![]()
![]()
![]()
![]()
Como en cualquier ejercicio de operaciones combinadas, el paréntesis me está indicando que primero resuelva la suma que está dentro, y luego multiplique el resultado por la fracción que está
fuera del paréntesis. Antes de multiplicar factorizo y simplifico lo que se pueda.
EXPLICACIÓN DEL EJEMPLO 1
EJEMPLO 2:
![]()
![]()
1
![]() 1
1
![]()
![]()
![]()
![]()
Son dos términos: una multiplicación en el primero, y el 1 en el segundo. Como en cualquier ejercicio de operaciones combinadas, se resuelve cada término y luego se suman o se restan.
EXPLICACIÓN DEL EJEMPLO 2



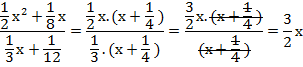
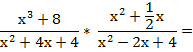
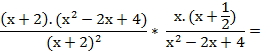
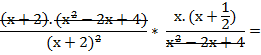
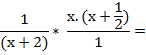
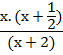
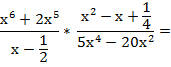
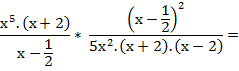
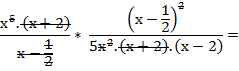 1
1