Tomado y adaptado de:
https://www.matesfacil.com/ESO/Ecuaciones/resueltos-sistemas-ecuaciones.html
UN Sistema de ecuaciones lineales es un conjunto de ecuaciones (lineales) que tienen más de una incógnita. Las incógnitas aparecen en varias de las ecuaciones, pero no necesariamente en todas. Lo que hacen estas ecuaciones es relacionar las incógnitas entre sí.
Ejemplo de un sistema:
Es un sistema de dos ecuaciones con dos incógnitas ( e .
Resolver un sistema de ecuaciones consiste en encontrar el valor de cada
incógnita para que se cumplan todas las ecuaciones del sistema.
La solución al sistema del ejemplo anterior es
Pero no siempre existe solución, o bien, pueden existir infinitas
soluciones. Si hay una única solución (un valor para cada incógnita,
como en el ejemplo anterior) se dice que el sistema es compatible
determinado. No hablaremos de los otros tipos ya que en esta
página sólo se estudian los sistemas determinados.
Para resolver un sistema (compatible determinado)
necesitamos tener al menos tantas ecuaciones como incógnitas.
No olvidemos que si multiplicamos una ecuación por un número
distinto de 0, la ecuación inicial y la obtenida son equivalentes.
Esto quiere decir que ambas ecuaciones tienen las mismas soluciones
y, por tanto, podemos trabajar con una u otra. Usaremos esta
propiedad con frecuencia en el método de reducción.
Sistemas Resueltos
Sistema 1

Despejamos en la primera ecuación la :
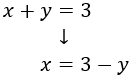
Y la sustituimos en la segunda:
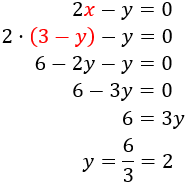
Calculamos sabiendo :
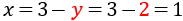
Por tanto, la solución del sistema es
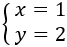
Despejamos en ambas ecuaciones la
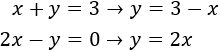
Como , igualamos las expresiones y resolvemos la ecuación:
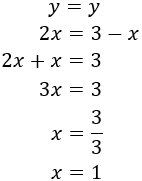
Ahora, sustituimos el valor de la incógnita en la primera de las ecuaciones anteriores para calcular :
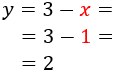
Por tanto, la solución del sistema es
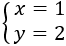
Sistema 2
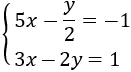
Despejamos en la segunda ecuación la :
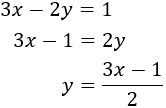
Sustituimos la expresión obtenida en la primera ecuación y la resolvemos:
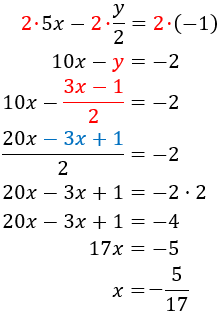
Como ya conocemos , calculamos sustituyendo en alguna de las ecuaciones anteriores:
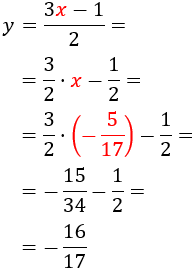
Por tanto, la solución del sistema es
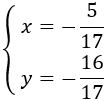
Despejamos en ambas ecuaciones la :
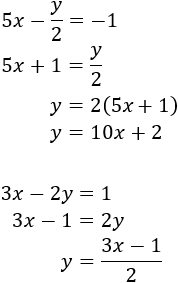
Igualamos las expresiones y resolvemos la ecuación:
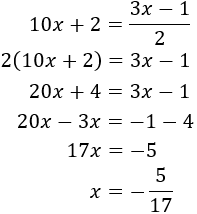
Sustituyendo en la primera de las ecuaciones anteriores obtenemos :
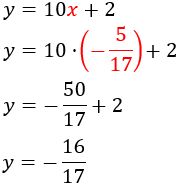
Por tanto, la solución del sistema es
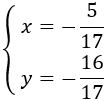
Multiplicamos la primera ecuación por 3 y la segunda por 5 para conseguir que el coeficiente de la incógnita tenga el mismo coeficiente en ambas ecuaciones:
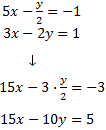
Cambiamos el signo a la segunda ecuación (la multiplicamos por -1) y sumamos las ecuaciones:

Sustituimos el valor de en la primera ecuación y la resolvemos:
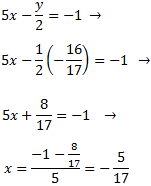
Por tanto, la solución del sistema es
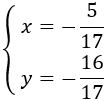
Sistema 3
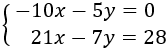
Despejamos en la primera ecuación la :
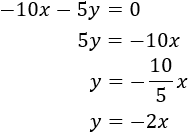
Sustituimos su expresión en la segunda ecuación y la resolvemos:
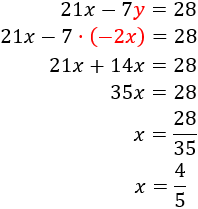
Calculamos sabiendo :
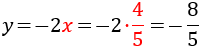
Por tanto, la solución del sistema es
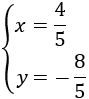
Despejamos en ambas ecuaciones la incógnita :
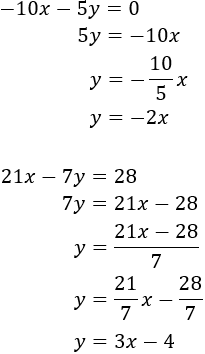
Igualamos las expresiones obtenidas y resolvemos la ecuación:
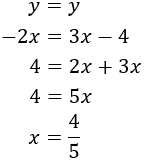
Sustituyendo en la primera de las ecuaciones anteriores obtenemos:
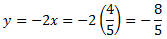
Por tanto, la solución del sistema es
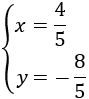
Multiplicamos la primera ecuación por la fracción 1/5 y la segunda por la fracción 1/7:
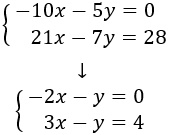
De este modo, evitamos coeficientes altos que complican las operaciones.
Ahora, multiplicamos la primera ecuación por 3, la segunda por 2 y las sumamos:
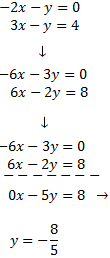
Sustituimos el valor de en la primera ecuación y la resolvemos:
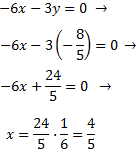
Por tanto, la solución del sistema es
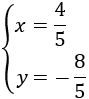
Sistema 4
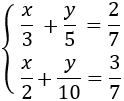
Despejamos de la primera ecuación la , pero, primero, multiplicamos la ecuación por el mínimo común múltiplo de los denominadores y, de este modo, evitamos las fracciones.
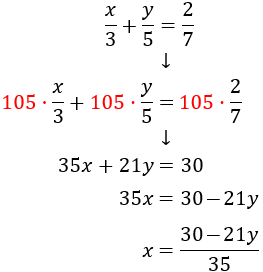
Sustituimos en la segunda ecuación la y la resolvemos. Primero, multiplicamos por el mínimo común múltiplo de los denominadores:
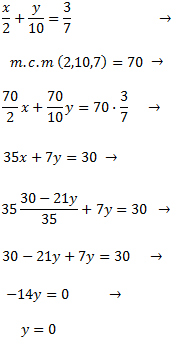
Calculamos sabiendo :
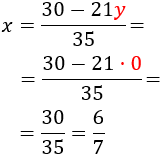
Por tanto, la solución del sistema es
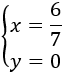
Multiplicamos cada ecuación por el mínimo común múltiplo de sus denominadores obteniendo las ecuaciones:
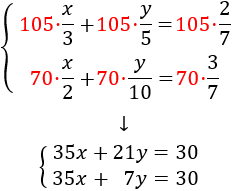
Despejamos en las dos ecuaciones la :
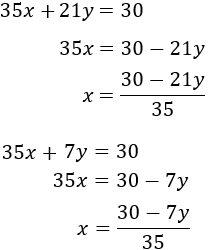
Igualamos ambas expresiones y resolvemos la ecuación:
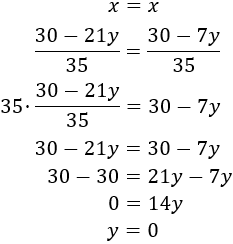
Sustituyendo en la primera de las ecuaciones anteriores,
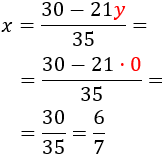
Por tanto, la solución del sistema es
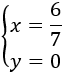
Multiplicamos cada ecuación por el mínimo común múltiplo de sus denominadores obteniendo las ecuaciones:
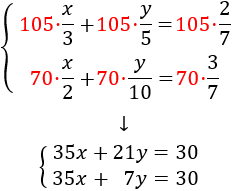
Multiplicamos la segunda por -1 y sumamos las ecuaciones:
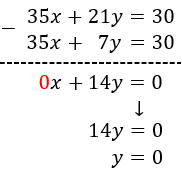
Sustituimos el valor en la primera ecuación y la resolvemos:
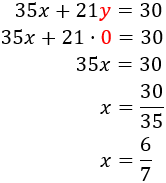
Por tanto, la solución del sistema es
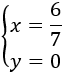
Sistema 1
Resolver gráficamente el siguiente sistema de ecuaciones:
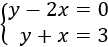
Lo primero que hacemos es despejar la en ambas ecuaciones.
Primera ecuación:
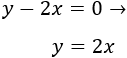
Segunda ecuación:
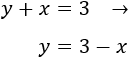
Ahora vamos a calcular unos cuantos puntos de las dos funciones para representarlas. Utilizaremos y .
Para la primera función tenemos la tabla
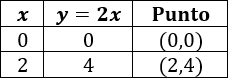
Para la segunda función tenemos la tabla
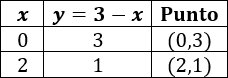
Ahora representamos los puntos de cada tabla uniéndolos:
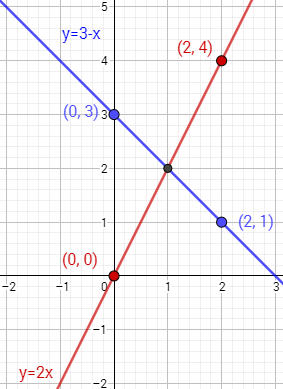
La solución del sistema es el punto donde las gráficas se cortan:
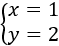
Sistema 2
Resolver gráficamente el siguiente sistema de ecuaciones:
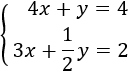
Lo primero que hacemos es despejar la en ambas ecuaciones.
Primera ecuación:
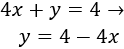
Segunda ecuación:
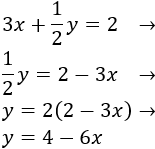
Ahora vamos a calcular unos cuantos puntos de las dos funciones para representarlas. Utilizaremos y .
Para la primera función tenemos la tabla

Para la segunda función tenemos la tabla

Ahora representamos los puntos de cada tabla uniéndolos:
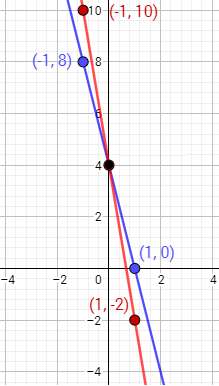
Sistema 3
Resolver gráficamente el siguiente sistema de ecuaciones:
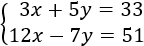
En este problema vamos a dar valores a la y a la directamente. Los puntos que escogemos son los puntos de corte con los ejes (es decir, e ).
En la primera ecuación, si , entonces
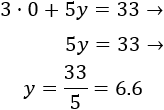
Y si , entonces
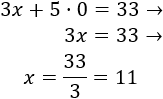
Por tanto, para la primera recta tenemos
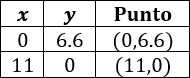
Repetimos el proceso con la segunda ecuación:
Si , entonces
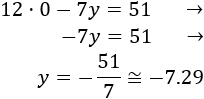
Y si , entonces
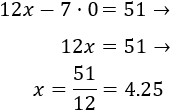
Por tanto, para la segunda recta tenemos
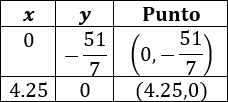
Ahora representamos los puntos de cada tabla uniéndolos:
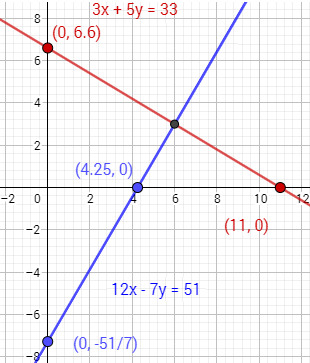
La solución del sistema es el punto donde las gráficas se cortan:
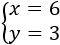
Sistema 4
Resolver gráficamente el siguiente sistema de ecuaciones:
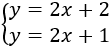
Como tenemos la despejada en ambas ecuaciones, damos valores a . Utilizamos y .
Para la primera función tenemos la tabla
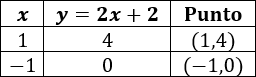
Para la segunda función tenemos la tabla

Ahora representamos los puntos de cada tabla uniéndolos:
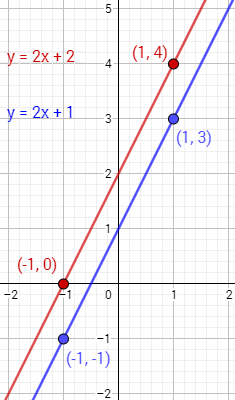
La solución del sistema es el punto donde las gráficas se cortan, pero las rectas de este problema no se cortan porque son paralelas (tienen la misma pendiente ). Por tanto, el sistema no tiene solución.
Sistema 5
Resolver gráficamente el siguiente sistema de ecuaciones:
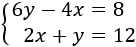
Lo primero que hacemos es despejar la en ambas ecuaciones.
Primera ecuación:
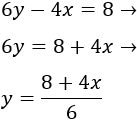
Segunda ecuación:
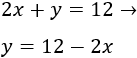
Ahora vamos a calcular unos cuantos puntos de las dos funciones para representarlas. Para la primera, utilizaremos y y para la primera la segunda, y .
La primera tabla que tenemos es

La segunda tabla es

Representamos y unimos los puntos de las rectas:
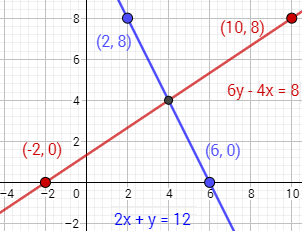
La solución del sistema es el punto donde las rectas se cortan:
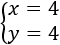
Sistema 6
Resolver gráficamente el siguiente sistema de ecuaciones:
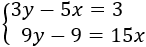
En este problema vamos a dar valores a y a sin despejar la . Calcularemos los puntos de corte con los ejes dando los valores e .
En la primera ecuación, si , entonces
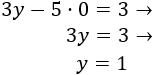
Y si , entonces
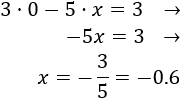
En la segunda ecuación, si , entonces
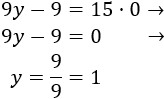
Y si , entonces
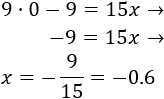
Para la primera función tenemos la tabla
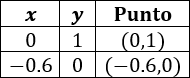
Para la segunda función tenemos la tabla
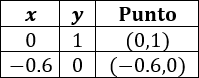
Los dos puntos obtenidos para cada función son los iguales. Esto significa que las rectas se cortan en dos puntos y, por tanto, las ecuaciones representan la misma recta. Recordad que la intersección entre dos rectas puede ser:
-
un único punto,
-
ningún punto (las rectas son paralelas) o
-
infinitos puntos (se trata de la misma recta).
En este problema estamos en el segundo caso.
Por tanto, el sistema de ecuaciones tiene infinitas soluciones.
La gráfica de las rectas del sistema es
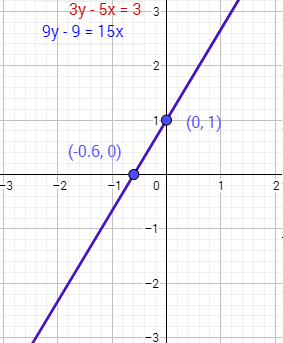
Sistema 7
Resolver gráficamente el siguiente sistema de inecuaciones:
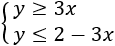
En este problema tenemos dos desigualdades.
Cada una de las desigualdades representa una región del plano. La solución del sistema es la intersección de ambas regiones. Por tanto, lo que haremos es representar las dos regiones por separado para observar la región en la que se cortan.
Para representar la región , representamos primero la recta . Podemos hacerlo dando puntos. La gráfica de la recta es
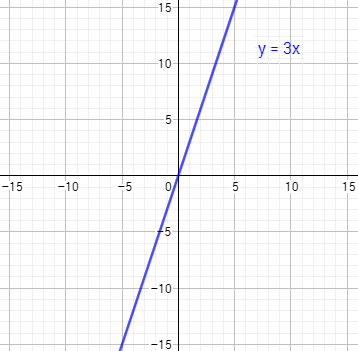
La recta divide el plano en dos regiones e es una de ellas. Para saber cuál, tomamos un punto de cada una y comprobamos cuál de los dos cumple la desigualdad .
Tomamos los puntos (-5,5) (lado izquierdo) y (5,-5) (lado derecho):
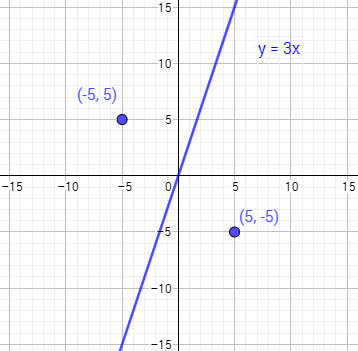
El punto que cumple la desigualdad es el primero ya que
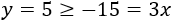
Por tanto, la región es la del lado izquierdo (color azul):
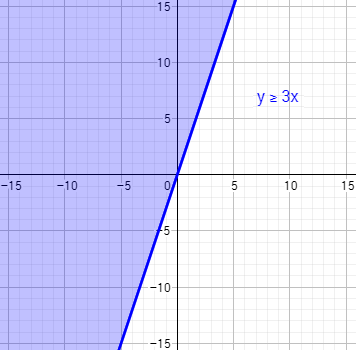
Repetimos el proceso con la región (región roja):
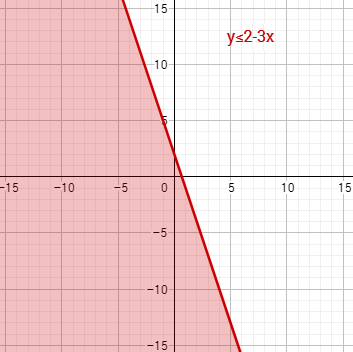
Ahora representamos ambas regiones y su intersección (color más oscuro) es la solución del sistema:
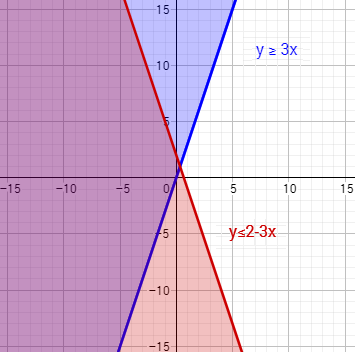
La solución del sistema de inecuaciones (o de desigualdades) es una región del plano y, por tanto, existen infinitos puntos que cumplen ambas inecuaciones.
Método de Determinantes o Kramer:
Un determinante es un arreglo de filas y columnas que se calcula así:
Determinante 1
Matriz de dimensión 2x2
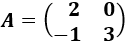
Determinante 2
Matriz de dimensión 2x2
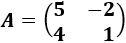
Procedemos del mismo modo:
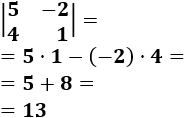
Determinante 3
Matriz de dimensión 2x2
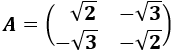
Procedemos del mismo modo:
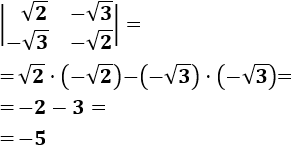
Determinante 4
Matriz de dimensión 3x3

Calculamos el determinante aplicando Sarrus:
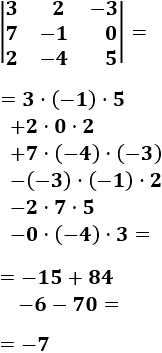
Sistema 1
Sistema 3x3
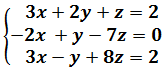
Calculamos el determinante de la matriz de coeficientes del sistema por la rega de Sarrus:
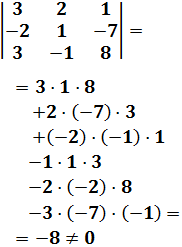
Como el determinante es distinto de 0, la matriz es regular y el sistema tiene una única solución (sistema compatible determinado):
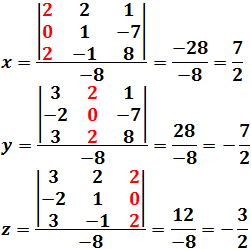
Nota: para calcular la incógnita asociada a la columna , sustituimos la columna de la matriz de coeficientes por la columna de términos independientes.
Sistema 2
Sistema 3x3
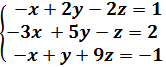
Calculamos el determinante de la matriz de coeficientes del sistema por Sarrus:
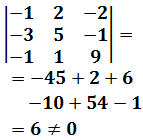
Podemos aplicar la regla de Cramer:
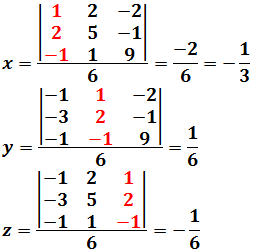
Sistema 3
Sistema 3x3
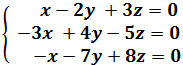
Calculamos el determinante de la matriz de coeficientes del sistema:
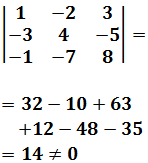
Podemos aplicar Cramer, pero como todos los términos independientes del sistema son 0, ya la solución:
Sistema 5
Sistema 3x3
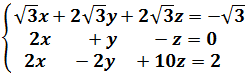
Calculamos el determinante de la matriz de coeficientes del sistema (aplicamos las propiedades de los determinantes):
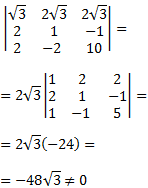
Resolvemos el sistema por Cramer:
Problemas Resueltos
Problema 1
Dos números suman 25 y el doble de uno de ellos es 14. ¿Qué números son?
x= primer número
y= segundo número
Los números suman 25:
x + y = 25
El doble de uno de los números es 14:
2x = 14
Tenemos el sistema
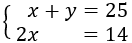
Aplicamos substitución
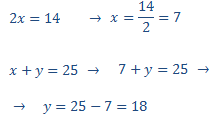
Por tanto, los números son 7 y 18.
Problema 2
El doble de la suma de dos números es 32 y su diferencia es 0. ¿Qué números son?
x= primer número
y= segundo número
El doble de la suma de los números es 32:
2(x + y) = 32
La diferencia de los números es 0:
x - y = 0
Tenemos el sistema
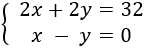
Aplicamos reducción
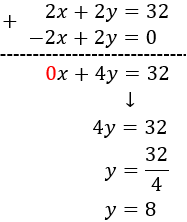
Por tanto, los números son 8 y 8.
Problema 3
La suma de dos números es 12 y la mitad de uno de ellos el doble del otro. ¿Qué números son?
x= primer número
y= segundo número
La suma de los números es 12:
x + y = 12
La mitad del primer número es el doble del segundo: x/2 = 2y
Tenemos el sistema
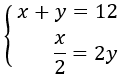
Resolvemos por substitución
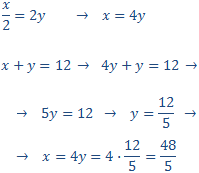
Por tanto, los números son 18/5 y 12/5.
Problema 4
Tenemos dos números cuya suma es 0 y si a uno de ellos le sumamos 123 obtenemos el doble del otro. ¿Qué números son?
x= primer número
y= segundo número
La suma de los números es 0: x + y = 0
Si al primero le sumamos 123 obtenemos el doble del segundo:
x + 123 = 2y
Tenemos el sistema
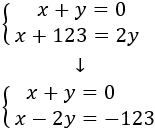
Resolvemos por substitución
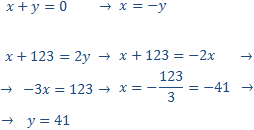
Por tanto, los números son 41 y -41.
Problema 5
Hallar un número de dos cifras que cumpla:
- La segunda cifra es el doble de la primera
- La suma de las cifras es 12.
El número es xy donde x es la primera cifra e y la segunda.
La segunda cifra es el doble de la primera:
y = 2x
La suma de las cifras es 12:
x + y = 12
Tenemos el sistema
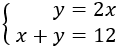
Resolvemos por substitución
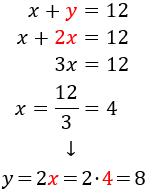
Por tanto, el número es 48.


