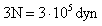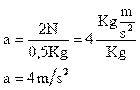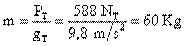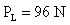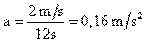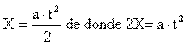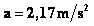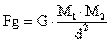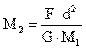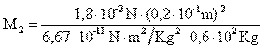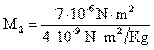LEYES DE NEWTON
Historia
La formulación matemática fue publicada por Isaac Newton en 1687,
en su obra Philosophiae Naturalis Principia Mathematica. Las leyes de Newton constituyen, junto con la transformación de Galileo, la base de la mecánica clásica. En el tercer volumen de
los Principia Newton mostró que, combinando estas leyes con su Ley de la gravitación universal, se pueden deducir y explicar las Leyes de Kepler sobre el
movimiento planetario.
Fundamentos teóricos de las leyes
Newton planteó que todos los movimientos se atienen a tres leyes principales formuladas en términos matemáticos y que implican conceptos que es necesario primero definir con rigor. El primer
concepto que maneja Newton es el de masa, que identifica con "cantidad de materia" otro concepto es la fuerza, causa del movimiento; los dos son denominados habitualmente por las
letras F y m.
Fuerza
- Causa del movimiento (F).
Masa
- Medición de la cantidad de materia puesta en movimiento (m).
Newton asume a continuación que la cantidad de movimiento es el resultado del producto de la masa por la velocidad. En tercer lugar, precisa la importancia de distinguir entre lo absoluto y
relativo siempre que se hable de tiempo, espacio, lugar o movimiento.
En este sentido, Newton, que entiende el movimiento como una traslación de un cuerpo de un lugar a otro, para llegar al movimiento absoluto y verdadero de un cuerpo compone el movimiento
(relativo) de ese cuerpo en el lugar (relativo) en que se lo considera, con el movimiento (relativo) del lugar mismo en otro lugar en el que esté situado, y así sucesivamente, paso a paso, hasta
llegar a un lugar inmóvil, es decir, al sistema de referencias de los movimientos absolutos.
De acuerdo con esto, Newton establece que los movimientos aparentes son las diferencias de los movimientos verdaderos y que las fuerzas son causas y efectos de estos. Consecuentemente, la fuerza
en Newton tiene un carácter absoluto, no relativo.
Las leyes
Primera ley de Newton o ley de la inercia
Todo cuerpo continúa en su estado de reposo, o de movimiento uniforme en una línea recta, a menos que sea obligado a cambiar ese estado por fuerzas aplicadas sobre él. [1]
El movimiento es relativo, es decir, depende de cual sea el observador que describa el movimiento. Así, para un pasajero A sentado un tren, otro pasajero B también sentado esta en reposo,
mientras que para alguien que ve pasar el tren desde el andén de una estación, tanto el pasajero A como el B se están moviendo a una gran velocidad. Se necesita, por tanto, un sistema de
referencia al cual referir el movimiento.
La primera ley de Newton sirve para definir un tipo especial de sistemas de referencia conocidos como Sistemas de referencia inerciales, que son aquellos sistemas de referencia desde los que se
observa que un cuerpo sobre el que no actúa ninguna fuerza neta se mueve con velocidad constante.
En realidad, es imposible encontrar un sistema de referencia inercial, puesto que siempre hay algún tipo de fuerzas actuando sobre los cuerpos, pero siempre es posible encontrar un sistema de
referencia en el que el problema que se está estudiando se pueda tratar como si se estuviera en un sistema inercial. En muchos casos, suponer a un observador fijo en la Tierra es una buena
aproximación de sistema inercial.
Ejemplo
Un buen ejemplo en el que se aprecia esta fuerza, es cuando un ómnibus se detiene de manera brusca, si las personas en el ómnibus no se encuentran sujetas continuarán su movimiento rectilíneo (se
desplazarán hacia adelante), si por el contrario el ómnibus esta detenido y comienza a moverse bruscamente la tendencia será a mantener el estado de reposo (se desplazarán hacia atrás)
Segunda ley de Newton o ley de fuerza
La fuerza define la dirección en que el cuerpo se pone en movimiento o cambia dicho movimiento. Ambas, fuerza y masa, determinan la rapidez con que el cuerpo cambia su reposo o movimiento: cuanto
mayor sea la fuerza aplicada y menor la masa del cuerpo, mayor será dicha rapidez.[1]
Esta ley se encarga de cuantificar el concepto de fuerza. En términos matemáticos se expresa mediante la relación:
F = m • a
Tanto la fuerza como la aceleración son magnitudes vectoriales, es decir, tienen, además de un valor, una dirección y un sentido. De esta manera, la Segunda ley de Newton debe expresarse
como:
→ →
F = m • a
La unidad de fuerza en el Sistema Internacional es el Newton y se representa por N. Un Newton es la fuerza que hay que ejercer sobre un cuerpo de un kilogramo de masa para que
adquiera una aceleración de 1 m/s2, o sea,
1 N = 1 Kg • 1 m/s2
La expresión de la Segunda ley de Newton que hemos dado es válida para cuerpos cuya masa sea constante. Si la masa varia, como por ejemplo un cohete que va quemando combustible, no es válida la
relación F = m • a.
Vamos a generalizar la Segunda ley de Newton para que incluya el caso de sistemas en los que pueda variar la masa. Para ello primero vamos a definir una magnitud física nueva. Esta magnitud
física es la cantidad de movimiento que se representa por la letra p y que se define como el producto de la masa de un cuerpo por su velocidad, es decir:
p = m • v
La cantidad de movimiento también se conoce como momento lineal. Es una magnitud vectorial y, en el Sistema Internacional se mide en Kg•m/s .
En términos de esta nueva magnitud física, la Segunda ley de Newton se expresa de la siguiente manera:
La Fuerza que actúa sobre un cuerpo es igual a la variación temporal de la cantidad de movimiento de dicho cuerpo, es decir,
F = dp/dt
De esta forma incluimos también el caso de cuerpos cuya masa no sea constante
Tercera ley de Newton o ley de acción
y reacción
Si un cuerpo A ejerce una fuerza sobre otro B, entonces, el cuerpo B ejercerá una fuerza sobre el A, de igual valor; pero en sentido contrario. [1]
Matemáticamente la tercera ley del movimiento de Newton suele expresarse como sigue:
F1 = F2'
donde F1 es la fuerza que actúa sobre el cuerpo 1 y F2' es la fuerza reactiva que actúa sobre el cuerpo 2
Ejemplo
Cuando en una piscina un bañista A empuja a otro bañista B, ambos se desplazan en sentido contrario aunque este último no haga el intento de empujar al primero. Esto
se debe a la reacción que el bañista B hace sobre el bañista A.
Es importante observar que este principio de acción y reacción relaciona dos fuerzas que no están aplicadas al mismo cuerpo, produciendo en ellos aceleraciones diferentes, según sean sus masas.
Por lo demás, cada una de esas fuerzas obedece por separado a la segunda ley es decir aunque los pares de acción y reacción tenga el mismo valor y sentidos contrarios, no se anulan entre si,
puesto que actúan sobre cuerpos distintos.
Límites de validez de las leyes de Newton
Las leyes que constituyen las bases de la dinámica, se conocen bajo el nombre de leyes del movimiento mecánico y fueron formuladas en 1687 por
Isaac Newton, estas leyes permitieron comprender el comportamiento de los fenómenos mecánicos y dar explicación a otros como el movimiento de la Tierra alrededor del Sol, el movimiento de los
péndulos, de cuerpos suspendidos por muelles como determinar con exactitud el movimiento de los vehículos espaciales e incluso predecir su comportamiento, pero estas leyes tienen límite en su
validez.
La primera Ley de Newton o ley de la inercia
Esta primera ley solo se cumple para un Sistema Inercial y una partícula- punto material, para
entender dicho planteamiento se debe conocer que para estudiar el movimiento de un cuerpo, se analiza primero un sistema de referencia. Un mismo movimiento parece diferente si se observa desde
distintos sistemas de referencia. Un sistema se define como inercial si está en reposo o en Movimiento Rectilíneo Uniforme. Punto material, es la idealización
de un cuerpo al que suponemos con masa pero sin ocupar volumen lo que supone asignarle una densidad infinita (d= m/v ).
La segunda ley de Newton o ley de fuerza
Esta ley sólo se cumple en Sistemas Inerciales. (En Sistemas no Inerciales la fórmula válida es: F +Fi = m•a), para masas no muy pequeñas (que no tengan implicaciones cuánticas) y para
velocidades pequeñas v <<< c (velocidad de la luz). Según la Dinámica clásica una fuerza actuando sobre un cuerpo le comunica una aceleración a= cte, pero la velocidad crece
indefinidamente v = a•t . Si esto fuera así en un tiempo infinito la velocidad sería infinita, lo cual está en desacuerdo con la experiencia y está explicado en la mecánica relativista que le
pone un límite a V= 3•10 8 m/s.
La tercera ley de Newton o ley de acción y reacción
Las fuerzas proceden de una interacción y siempre aparecen de dos en dos. Se aplica cada una en uno de los cuerpos que interaccionan, (sí se aplicaran las dos en el mismo cuerpo producirían
reposo). Para obtener equilibrio se requiere dos o más interacciones sobre un cuerpo para que las fuerzas originadas se anulen.
Sólo se cumple la tercera Ley si el tiempo de interacción es suficientemente largo para que se establezca la respuesta a la acción.
Al resolver los problemas de dinámica, se aplican las leyes de Newton sin pensar si ellas son válidas en todos los casos, tampoco se tiene en cuenta si el sistema de referencia en que se analiza
el movimiento de los cuerpos puede influir al operar con dichas leyes, o si los valores de las velocidades a que se mueven los cuerpos, pueden limitar la aplicación de ellas, incluso se habla de
cuerpos que son considerados como punto material, que como resultado de las interacciones solo experimentan variaciones en su movimiento de traslación.
- Un conductor de un automóvil frena de manera brusca y, por inercia, sale disparado hacia adelante.
- Una piedra en el suelo se encuentra en estado de reposo.
- Una bicicleta guardada hace cinco años en un desván sale de su estado de inercia cuando un niño se decide a usarla.
- Un maratonista sigue corriendo varios metros más allá de la línea de llegada debido a la inercia de su carrera.
Ejemplos de la segunda ley de Newton
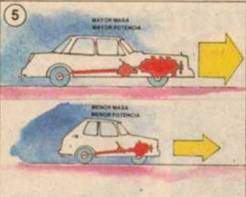
- Una señora enseña a andar en bicicleta a dos niños: uno de 4 años y otro de 10 años, para que lleguen al mismo lugar, deberá ejercer más fuerza al empujar al niño de 10 años pues su peso es
mayor.
- Un auto necesita cierta cantidad de caballos de fuerza para poder circular en la carretera.
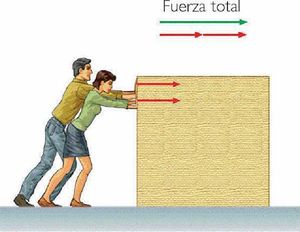
- Empujar un auto averiado entre más personas hará que el auto se mueva a mayor velocidad.
Ejemplos de la tercera ley de Newton
- Si una bola de billar golpea a otra, la segunda se desplazará con la misma fuerza con la que se desplaza la primera.
- Un niño quiere dar un salto para treparse a un árbol (reacción), debe empujar el suelo para impulsarse (acción).
- Un hombre desinfla un globo; la fuerza con la que sale el aire hace que el globo se mueva de un lado hacia otro.
Informacion complementaria Leyes de Newton
Tomada de:https://www.todamateria.com/leyes-de-newton/
Las leyes del movimiento de Newton describen la relación entre las fuerzas que actúan sobre un cuerpo y el movimiento de este cuerpo debido a dichas
fuerzas. Estas constituyen los principios fundamentales usados para analizar el movimiento de los cuerpos y son la base de la mecánica clásica.
Las tres leyes de Newton fueron publicadas en 1687 por Isaac Newton (1643-1727) en su obra Principios matemáticos de la filosofía
natural (Philosophiae Naturalis Principia Mathematica).
Primera ley de Newton: ley de la inercia
La primera ley de Newton establece que si la resultante de las fuerzas ejercidas sobre un cuerpo es nula, el cuerpo permanecerá en reposo si estaba en reposo inicialmente, o se mantendrá en
movimiento rectilíneo uniforme si estaba inicialmente en movimiento.
Así, para que un cuerpo salga de su estado de reposo o de movimiento rectilíneo uniforme, es necesario que una fuerza actúe sobre él.
La primera ley de Newton es llamada también “ley de la inercia” o “principio de la inercia”. La inercia es la tendencia de los cuerpos de
permanecer en reposo o en movimiento rectilíneo uniforme.
Por lo tanto, si la suma vectorial de las fuerzas es nula, resultará en el equilibrio de las partículas. Por otro lado, si hay fuerzas resultantes, producirá una variación en su velocidad.
Cuanto mayor sea la masa de un cuerpo, mayor será su tendencia de permanecer en reposo o en movimiento rectilíneo uniforme.
Ejemplo de la primera ley de Newton
Pensemos en un conductor que lleva un carro a una determinada velocidad, se atraviesa un perro delante del carro y el conductor frena rápidamente. En esta situación los pasajeros continúan el
movimiento y son lanzados hacia adelante.
Segunda ley de Newton: ley fundamental de la dinámica
La segunda ley de Newton es el principio fundamental de la mecánica y establece que la intensidad de la resultante de las fuerzas ejercidas en un cuerpo
es directamente proporcional al producto de la aceleración que adquiere por la masa del cuerpo:

Donde F es el resultante de las fuerzas que actúan sobre el cuerpo; m, la masa del
cuerpo; a, la aceleración del cuerpo.
En el sistema internacional las unidades de medida son:
Para F (fuerza): newtons (N).
Para m (masa): kilogramos (kg).
Para a (aceleración): metros por segundo al cuadrado (m/s2).
Es importante resaltar que la fuerza es un vector, es decir, posee módulo, dirección y sentido. Por lo tanto, cuando varias fuerzas actúan sobre un cuerpo, ellas se suman vectorialmente y el
resultado es la fuerza resultante.
La flecha sobre las letras en la fórmula representa que la fuerza y la aceleración son vectores y que la dirección y el sentido de la aceleración serán los mismos de la fuerza resultante.
Ejemplo de la segunda ley de Newton
Un carrito de mercado es más fácil de mover si está vacío, esto es, requiere menos fuerza para moverlo porque tiene menos masa. En cambio, si está lleno, cuesta más moverlo.
Tercera ley de Newton: ley de acción y reacción
La tercera ley de Newton es llamada ley de acción y reacción, en la cual a toda fuerza de acción le corresponde una fuerza de reacción.
De esta manera, las fuerzas de acción y reacción, que actúan en pares, no se equilibran, una vez que están aplicadas en cuerpos diferentes. Recordando que esas fuerzas presentan la misma magnitud
y dirección pero en sentido opuesto.
Ejemplo de la tercera ley de Newton
Una forma de ejemplificar la tercera ley de Newton podría ser la siguiente: hay dos patinadores, parados uno frente al otro. Si uno de ellos empuja al otro, ambos se moverán en sentidos opuestos.
Vea también Isaac Newton.
Puntos claves a recordar sobre las leyes de Newton
- Las tres leyes de Newton son la base de la mecánica.
- La fuerza resultante es la suma de todas las fuerzas que actúan sobre un objeto. Las fuerzas que son de igual
magnitud pero en sentidos opuestos se anulan.
- La aceleración de un objeto es proporcional a la fuerza aplicada sobre él.
- La fuerza causa que un objeto se mueva.
- Un objeto con mayor masa requiere más fuerza para moverse.
- La fricción es la fuerza entre los objetos y la superficie sobre la que se mueven.
- La inercia es la tendencia de un cuerpo en movimiento a permanecer en movimiento y depende de la masa.
Ejercicios de las leyes de Newton (con soluciones)
Ejercicio 1
Pregunta: Cuando no hay fuerzas resultantes sobre un objeto en movimiento, este llega al reposo debido a su inercia. ¿Verdadero o falso?
Respuesta: Falso. Si no se aplican fuerzas resultantes a un objeto en movimiento, su velocidad no cambia. La razón por la que los objetos dejan
de moverse es porque la fricción los frena. La inercia no es una fuerza. Es la tendencia de un objeto para resistir un cambio en su velocidad.
Ejercicio 2
Pregunta: Dos jóvenes están halando una cuerda en direcciones opuestas ¿Cuál es la fuerza “igual y en dirección opuesta” a la fuerza de la mano
de uno de los jóvenes que hala la cuerda según la tercera ley de Newton?
Respuesta: La fuerza de la cuerda que hala de la mano del joven en la dirección opuesta. ¿Por qué? Si el objeto A le aplica una fuerza al objeto
B, entonces la fuerza “igual y opuesta” es la fuerza que B aplica sobre A (misma magnitud, pero dirección opuesta). No se anulan entre sí porque actúan sobre dos cuerpos diferentes. La
tercera ley de Newton describe la fuerza de la cuerda que hala de la mano en dirección opuesta.
Ejercicio 3
Pregunta: Un astronauta percibe que se aleja lentamente de la estación espacial y la cuerda que lo conecta está rota. En sus manos tiene un
equipo de 5 kg. ¿Qué podría hacer el astronauta de forma rápida?
Respuesta: Debería lanzar el equipo en la misma dirección a la que se va alejando. Por la tercera ley de Newton, el equipo aplicará la misma
fuerza en dirección opuesta, o sea, hacia la estación espacial.
Ejercicio 4
Pregunta: En un experimento el bloque I (m=10 kg) y el bloque II (m=6 kg) están conectados por una cuerda ideal. En un primer momento, se aplica
una fuerza de magnitud igual a 64N en el bloque I, generando en la cuerda una tensión TA. Luego, se aplica una fuerza de la misma magnitud F en el bloque II, produciendo una tensión TB, como se
muestra en el esquema.

Si consideramos despreciable la fricción entre los bloques y la superficie, la relación entre las tensiones corresponde a:
a) 9/10
b) 4/7
c) 3/5
d) 8/13
Respuesta correcta: Opción c.
Ejercicio 5
Pregunta: En el interior de un avión que se desplaza horizontalmente con relación al suelo, con velocidad constante de 1000 km/h, un pasajero
deja caer un vaso. Observe la figura en la cual están indicados cuatro puntos en el piso del corredor del avión y la posición del pasajero. ¿Sobre cuál de los puntos marcados cae el
vaso?

Respuesta: Sobre el punto R.
Pasos para resolver problemas de las leyes de Newton
Paso 1
Identifica los principios físicos involucrados. Dibuja un esquema de la situación. Usa flechas para mostrar las fuerzas, su dirección y magnitud.

Paso 2
Identifica lo que se pide en el problema y cuáles son los datos conocidos o que se pueden inferir del problema. Luego determina el sistema de interés. Este paso es crítico, ya que la segunda ley
de Newton sólo considera las fuerzas externas. La tercera ley de Newton se puede usar si las fuerzas se ejercen entre componentes de un sistema (interno) o entre el sistema y algo en el exterior
(externo).
Dibuja un diagrama de cuerpo libre donde muestras el sistema de interés y las fuerzas externas (no se coloca velocidad o aceleración).
Paso 3
Una vez que las fuerzas externas están claramente identificadas en un diagrama de cuerpo libre, se puede escribir la ecuación para determinar el parámetro desconocido. Si el problema es de una
dimensión —es decir, las fuerzas son paralelas— entonces se suman los escalares. Si el problema es bidimensional, debe ser separado en sus componentes de una dimensión. Esto se hace proyectando
los vectores de las fuerzas en un set de ejes escogidos a conveniencia. Por ejemplo, cuando el problema tiene un plano inclinado, se representa un eje paralelo al la diagonal, y otro
perpendicular.
Paso 4
Revisa la solución para ver si es razonable. En la mayoría de los casos es obvio. Por ejemplo, cuando hay fricción se enlentece el deslizamiento de un objeto en plano inclinado. Otra forma de
revisar la solución es revisar las unidades: si el parámetro desconocido es Fuerza y las unidades son kg, evidentemente hay un error.

Ejemplo de problemas relacionados con la
Segunda Ley de Newton.
- 1. Una fuerza le proporciona
a la masa de 2,5 Kg. una aceleración de 1,2 m/s2. Calcular la magnitud de dicha fuerza en Newton y dinas.
Datos
m = 2,5 Kg.
a =1,2 m/s2.
F =? (N y dyn)
Solución
Nótese que los datos aparecen en un
mismo sistema de unidades
(M.K.S.)
Para calcular la fuerza usamos
la ecuación de la segunda ley de Newton:
 Sustituyendo valores tenemos:
Sustituyendo valores tenemos:

Como nos piden que lo expresemos
en dinas, bastará con multiplicar por 105, luego:
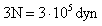
- 2. ¿Qué aceleración adquirirá
un cuerpo de 0,5 Kg. cuando sobre él actúa una fuerza de 200000 dinas?
Datos
a =?
m = 2,5 Kg.
F = 200000 dyn
Solución
La masa está dada en M.K.S., en cambio la fuerza está dada en c.g.s.
Para trabajar con M.K.S. debemos transformar la fuerza a la unida M.K.S. de esa magnitud (N)
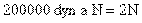
La ecuación de la segunda ley de Newton viene dada por:
 Despejando a tenemos:
Despejando a tenemos:
 Sustituyendo sus valores se tiene:
Sustituyendo sus valores se tiene:
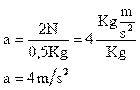
- 3. Un cuerpo pesa en la
tierra 60 Kp. ¿Cuál será a su peso en la luna, donde la gravedad es 1,6 m/s2?
Datos
PT= 60 Kp = 588 N
PL =?
gL = 1,6 m/s2
Solución
Para calcular el peso en la luna usamos la ecuación

Como no conocemos la masa, la calculamos por la ecuación: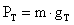 que al despejar m tenemos:
que al despejar m tenemos:
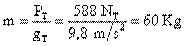
Esta masa es constante en cualquier parte, por lo que podemos usarla en la ecuación (I):
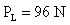
- 4. Un ascensor pesa 400 Kp.
¿Qué fuerza debe ejercer el cable hacia arriba para que suba con una aceleración de 5 m/s2? Suponiendo nulo el roce y la masa del ascensor es de 400 Kg.
Solución
Como puede verse en la figura 7, sobre el ascensor actúan dos fuerzas: la fuerza F de tracción del cable y la fuerza P del peso, dirigida hacia abajo.

La fuerza resultante que actúa sobre el ascensor es F – P
Aplicando la ecuación de la segunda ley de Newton tenemos:

Al transformar 400 Kp a N nos queda que:
400 Kp = 400 ( 9,8 N = 3920 N
Sustituyendo los valores de P, m y a se tiene:
F – 3920 N = 400 Kg. ( 0,5 m/s2
F – 3920 N = 200 N
Si despejamos F tenemos:
F = 200 N + 3920 N
F = 4120 N
- 5. Un carrito con su carga
tiene una masa de 25 Kg. Cuando sobre él actúa, horizontalmente, una fuerza de 80 N adquiere una aceleración de 0,5 m/s2. ¿Qué magnitud tiene la fuerza de rozamiento Fr que se opone al avance
del carrito?
Solución
En la figura 8 se muestran las condiciones del problema
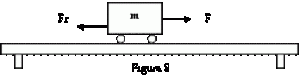
La fuerza F, que actúa hacia la derecha, es contrarrestada por la fuerza de roce Fr, que actúa hacia la izquierda. De esta forma se obtiene una resultante F – Fr que es la fuerza que produce
el movimiento.
Si aplicamos la segunda ley de Newton se tiene:
Sustituyendo F, m y a por sus valores nos queda
80 N – Fr = 25 Kg. ( 0,5 m/s2
80 N – Fr = 12,5 N
Si despejamos Fr nos queda:
Fr = 80 N – 12,5 N
Fr = 67,5 N
- 6. ¿Cuál es la fuerza
necesaria para que un móvil de 1500 Kg., partiendo de reposo adquiera una rapidez de 2 m/s2 en 12 s?
Datos
F =?
m = 1500 Kg.
Vo = 0
Vf = 2 m/s2
t = 12 s
Solución
Como las unidades están todas en el sistema M.K.S. no necesitamos hacer transformaciones.
La fuerza que nos piden la obtenemos de la ecuación de la segunda ley de Newton: 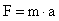
De esa ecuación conocemos la masa, pero desconocemos la aceleración. Esta podemos obtenerla a través de la ecuación

Porque partió de reposo.
Sustituyendo Vf y t por sus valores tenemos:
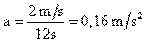
Si sustituimos el valor de a y de m en la ecuación (I) tenemos que:

- 7. Calcular la masa de un
cuerpo, que estando de reposo se le aplica una fuerza de 150 N durante 30 s, permitiéndole recorrer 10 m. ¿Qué rapidez tendrá al cabo de ese tiempo?
Datos
m =?
Vo = 0
F = 150 N
t = 30 s
x = 10 m
Vf =?
Solución
Como nos piden la masa, despejamos la segunda la segunda ley de Newton:

Como no se conoce la aceleración y nos dan la distancia que recorre partiendo de reposo, usamos la ecuación de la distancia en función del tiempo y despejamos (a)
Sustituyendo valores tenemos:

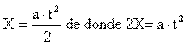
Sustituyendo los valores de X y t en (II) tenemos:
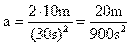
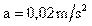 Sustituyendo a y F por sus valores en (I):
Sustituyendo a y F por sus valores en (I):

Tercera ley de newton.
-
1. Consideramos un
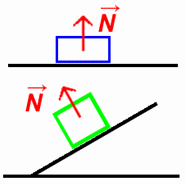
cuerpo con un masa m = 2 Kg. que está en reposo sobre un plano horizontal, como el indicado en la figura 17. a) Haz un diagrama de cuerpo libre. b) Calcular la fuerza con que el plano
reacciona contra el bloque.

Solución
a) Las fuerzas que
actúan sobre el bloque están representadas en la figura 18, donde se elije un eje de coordenadas cuyo origen es el centro del cuerpo, mostrándose las fuerzas verticales: el peso y la normal
y la normal 
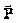 El peso del
cuerpo, dirección vertical y sentido hacia abajo.
El peso del
cuerpo, dirección vertical y sentido hacia abajo.
 Normal, fuerza
que el plano ejerce sobre el bloque.
Normal, fuerza
que el plano ejerce sobre el bloque.
Al diagrama así mostrado se le llama diagrama de cuerpo libre.
b) Para calcular la
fuerza que el plano ejerce sobre el bloque aplicamos la segunda ley de Newton:
Como  actúa hacia
arriba y
actúa hacia
arriba y 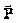 actúa hacia
abajo, la resultante viene dada en módulo por N – P, que al aplicar la segunda ley de Newton escribimos:
actúa hacia
abajo, la resultante viene dada en módulo por N – P, que al aplicar la segunda ley de Newton escribimos:
N – P = m . a
Como en la dirección vertical no hay movimiento entonces la aceleración es cero (a = 0), luego
N – P = 0
N = P
N = m . g (porque P = m ( g)
Sustituyendo los valores de m y g se tiene:
N = 2 Kg . 9,8 m/s2
N = 19,6 N
Esta es la fuerza con que el plano reacciona sobre el bloque.
-
2. En la figura 19
se muestran dos masas M1 = 3 Kg. y M2 = 5 Kg. colgando de los extremos de un hilo que pasa por la garganta de una polea a) Hacer un diagrama de las fuerzas que actúan b) Calcular la
tensión del hilo y la aceleración con que se mueve el sistema.

Solución
a) Obsérvese la figura
20(a), la cual representa el diagrama del cuerpo libre para el cuerpo de masa M1.
 Es la tensión del hilo, actuando hacia arriba.
Es la tensión del hilo, actuando hacia arriba.
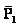 El peso del cuerpo de masa M1.
El peso del cuerpo de masa M1.
En la figura 20(b) se muestra el diagrama de cuerpo libre para el cuerpo de masa M2.
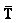 Es la tensión
del hilo, actuando hacia arriba.
Es la tensión
del hilo, actuando hacia arriba.
 El peso del cuerpo de masa M2.
El peso del cuerpo de masa M2.
b) Como el cuerpo de
masa M1 sube, la tensión T es mayor que P, por lo que podemos escribir en módulo la segunda ley de Newton así:
T – P1 = M1 . a.………………………………………… (A)
Como el cuerpo de masa M2 baja, el peso P2 es mayor que T, pudiéndose escribir en módulo la segunda ley de Newton así:
P2 – T = M2 . a.………………………………………… (B)
Despajando T de la ecuación (A) nos queda que:
T = M1 . a + P1
Sustituyendo ésta expresión en (B) tenemos:
P2 – (M1 . a + P1) = M2 . a
P2 – P1 = M2 . a + M1 . a
Sacando a como
factor común:
P2 – P1 = a . (M2 + M1)
Despejando nos queda:
 (C)
(C)
Calculemos por separado P1 y P2
P1 = M1 . g = 3 Kg . 9,8 m/s2
P1 = 29,4 N
P2 = M2 . g = 5 Kg. . 9,8 m/s2
P2 = 49 N
Sustituyendo todos los valores conocidos en la expresión (C) nos queda que:
La tensión la obtenemos sustituyendo en la expresión:
T = M1 . a + P1
T = 3 Kg . 2,45 m/s2 + 29,4 N
T = 7,35 N + 29,4 N
T = 36,4 N
Luego  y T = 36,4 N
y T = 36,4 N
-
3. En la figura 21
se muestran dos bloques de masa M2 = 2 Kg. que arrastra sobre el plano horizontal al cuerpo de masa M1 = 7 Kg. Calcular la aceleración del sistema y tensión de la cuerda.
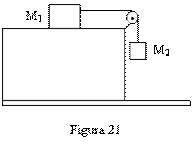
Solución
Antes debemos hacer un diagrama del cuerpo libre.
Para el bloque horizontal se muestra la figura 21(a) y para el bloque vertical el diagrama de la figura 21(b).

Horizontalmente se desplaza hacia la derecha y la única fuerza que actúa es la tensión, por lo que puede escribirse de acuerdo con la segunda ley de Newton que:
T = M1 . a.………………………….…………….….… (I)
En el bloque de masa M2, se lleva a cabo un movimiento vertical hacia abajo, pudiéndose escribir que:
P2 – T = M2 . a.………………………………………… (II)
Sustituyendo T de la ecuación (I) en (II) se tiene:
P2 – M1 . a = M2 ( a
Transponiendo términos se tiene que:
P2 = M2 . a + M1 ( a
Sacando a como
factor común:
P2 = a . (M2 + M1)
Despejando nos queda:

Sustituyendo todos los valores conocidos en la expresión (C) nos queda que:

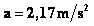
La tensión de la cuerda la obtenemos sustituyendo en la expresión:
T = M1 . a = 2Kg. ( 2,17 m/s2
T = 4,34 N
Ley de gravitación
universal.
-
1. Hallar la fuerza
con que se atraen dos masas de 5,5 ( 1024 Kg. y 7,3 ( 1022 Kg. separados por una distancia de 3,8 ( 108 m.
Solución
F = ?
M1 = 5,5 . 1024 Kg.
M2 = 7,3 . 1022 Kg.
d = 3,8 . 108 m
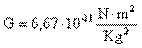
Para calcular la fuerza de atracción entre las masas M1 y M2, sustituimos en la fórmula de la cuarta ley de Newton el valor de cada una de ellas, así como los valores de G, y de la distancia d:
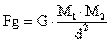
Quedando la fórmula como sigue:
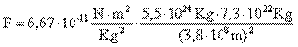



-
2. Calcular la masa
de un cuerpo, si fuerza de atracción entre dos masas es de 1,8 ( 10-2 N y la masa de una de ellas 0,6 ( 102 Kg., y las separa una distancia de 0,2 ( 10-1 m.
Solución
F = 1,8 ( 10-2 N
M1 = 0,6 ( 102 Kg.
M2 =?
d = 0,2 ( 10-1 m
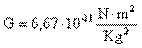
Despejando M2 de la fórmula de la cuarta ley de Newton tenemos
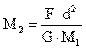
Sustituyendo en la fórmula los valores tenemos:
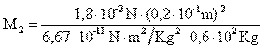
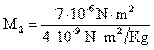


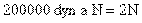
 Sustituyendo sus valores se tiene:
Sustituyendo sus valores se tiene:
![]() que al despejar m tenemos:
que al despejar m tenemos:


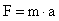


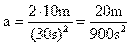
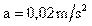 Sustituyendo a y F por sus valores en (I):
Sustituyendo a y F por sus valores en (I):

 y la normal
y la normal 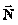
![]() El peso del
cuerpo, dirección vertical y sentido hacia abajo.
El peso del
cuerpo, dirección vertical y sentido hacia abajo.
![]() Normal, fuerza
que el plano ejerce sobre el bloque.
Normal, fuerza
que el plano ejerce sobre el bloque.
![]() actúa hacia
arriba y
actúa hacia
arriba y ![]() actúa hacia
abajo, la resultante viene dada en módulo por N – P, que al aplicar la segunda ley de Newton escribimos:
actúa hacia
abajo, la resultante viene dada en módulo por N – P, que al aplicar la segunda ley de Newton escribimos:
 Es la tensión del hilo, actuando hacia arriba.
Es la tensión del hilo, actuando hacia arriba.
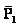 El peso del cuerpo de masa M1.
El peso del cuerpo de masa M1.
![]() Es la tensión
del hilo, actuando hacia arriba.
Es la tensión
del hilo, actuando hacia arriba.
 El peso del cuerpo de masa M2.
El peso del cuerpo de masa M2.





 Ver más ejemplos en:
Ver más ejemplos en: