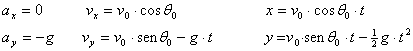TIRO PARABÓLICO
Se denomina movimiento parabólico al realizado por un objeto cuya trayectoria describe
una parábola. Se corresponde con la trayectoria ideal de un proyectil que se mueve en un medio que no ofrece resistencia al avance y que está sujeto a
un campo gravitatorio uniforme.
En realidad, cuando se habla de cuerpos que se mueven en un campo gravitatorio central (como el de La Tierra), el movimiento es elíptico. En la superficie de la Tierra, ese movimiento es tan parecido a una parábola que perfectamente podemos calcular su trayectoria usando la ecuación matemática de una parábola. La ecuación de una elipse es bastante más compleja. Al lanzar una piedra al aire, la piedra intenta realizar una elipse en uno de cuyos focos está el centro de la Tierra. Al realizar esta elipse inmediatamente choca con el suelo y la piedra se para, pero su trayectoria es en realidad un "trozo" de elipse. Es cierto que ese "trozo" de elipse es casi idéntico a un "trozo" de parábola. Por ello utilizamos la ecuación de una parábola y lo llamamos "tiro parabólico". Si nos alejamos de la superficie de la Tierra sí tendríamos que utilizar una elipse(como en el caso de los satélites artificiales).
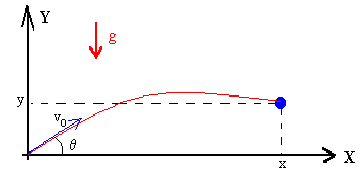
El movimiento parabólico puede ser analizado como la composición de dos movimientos rectilíneos: un movimiento rectilíneo uniforme horizontal y un movimiento rectilíno uniformemente acelerado vertical.
(http://es.wikipedia.org/wiki/Movimiento_parab%C3%B3lico)
|
La composición de un movimiento uniforme y otro uniformemente acelerado resulta un movimiento cuya trayectoria es una parábola.
Este movimiento está estudiado desde la antigüedad. Se recoge en los libros más antiguos de balística para aumentar la precisión en el tiro de un proyectil. Denominamos proyectil a todo cuerpo que una vez lanzado se mueve solo bajo la aceleración de la gravedad.
|
|||||||||||||||||||

EJERCICOS RESUELTOS CORRESPONDIENTES AL TALLER DE TIRO PARABOLICO
(al final encontraran el archivo descargable en pdf)







ACTIVIDAD
Sobre los temas vistos de cinemática deben realizar.
1. Tres ejercicios de movimiento rectilineo en el eje X.
2. Tres ejercicios de caida libre (eje Y).
3. Tres ejercicios de movimiento parabólico.
4. Tres ejercicios de movimiento circular.
PARA EL PROXIMO FIN DE SEMANA TENDREMOS LA EVALUACIÓN SOBRE ESTOS TEMAS.