TOMADO Y ADAPTADO DE : https://www.matesfacil.com/resueltos-ecuaciones-segundo-grado-incompletas.html
Vamos a resolver ecuaciones de segundo grado incompletas de los tres tipos. Recordemos que una ecuación de segundo grado, completa o no, puede tener, a lo sumo, dos raíces (reales) distintas.
Aquí podemos acceder a la sección de ecuaciones de segundo grado completas.
1. Ecuación Incompleta
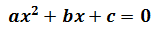
Una ecuación de segundo grado puede escribirse en la forma
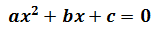
Decimos que la ecuación es completa cuando ninguno de los coeficientes, a,b y c es cero, es decir, cuando
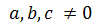
Y decimos que
La ecuación es incompleta cuando alguno de los coeficientes b ó c es cero.
Es decir, es incompleta cuando
Nota: no consideramos el caso en que a = 0 ya que, entonces, la ecuación no es de segundo grado.
Por tanto, una ecuación incompleta toma alguna de las siguientes formas
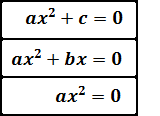
2. Obtención de las Soluciones (según los tipos)
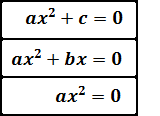
Vamos a ver cómo obtener las soluciones (raíces) en cada uno de los tres tipos de ecuaciones:
-
Si es de la forma
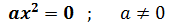
Tenemos la única solución (raíz doble) .
-
Si es de la forma
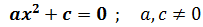
Despejando tenemos que
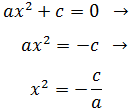
Haciendo la raíz cuadrada, obtenemos las dos raíces
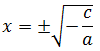
Pero es necesario que el radicando (interior de la raíz) sea no negativo. Si no es así, no existen soluciones (reales).
-
Si es de la forma
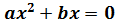
Factorizamos
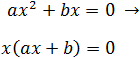
Como es un producto cuyo resultado es 0, alguno de los dos factores tiene que ser 0. Por tanto, tenemos las siguientes posibilidades (raíces):
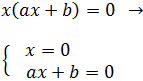
Es decir, una solución es
y la otra solución es
Resolución de Ecuaciones de Segundo Grado Incompletas
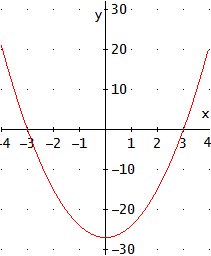
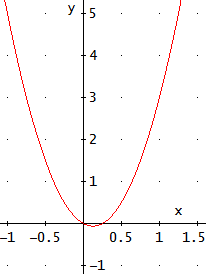
Nota: en la resolución de las ecuaciones mostramos la gráfica de la parábola que representa la ecuación. Es decir, la función
Como las soluciones de la ecuación son los puntos donde es 0, los puntos de corte de la parábola con el eje de abscisas están en los puntos cuya primera coordenada es la solución de la ecuación y la segunda coordenada es 0. Además, si , entonces la parábola tiene forma de U; si no, tiene forma de U invertida.
Ecuación 1
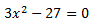
Despejamos x y hacemos la raíz cuadrada (no olvidemos el doble signo)
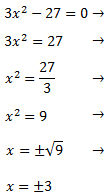
La ecuación tiene dos raíces y la podemos escribir en forma factorizada como
Ecuación 2
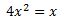
Factorizamos la expresión y nos queda un producto de x por una ecuación.
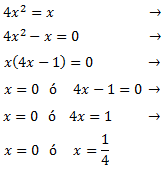
La ecuación tiene dos raíces y la podemos escribir en forma factorizada como
Ecuación 3
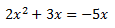
Factorizamos la expresión y nos queda un producto de x por una polinomio de primer grado. Por tanto, el producto es 0 si uno de los dos factores es 0:
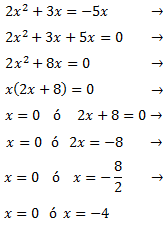
La ecuación tiene dos raíces y la podemos escribir en forma factorizada como
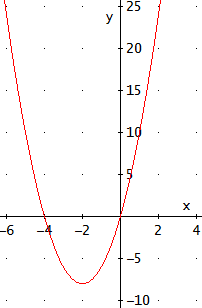
Ecuación 4
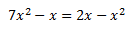
Agrupamos los monomios según su parte literal. Factorizamos la expresión y nos queda un producto de x por un polinomio de primer grado. Por tanto, el producto es 0 si x = 0 o el polinomio es 0:
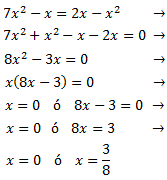
La ecuación tiene dos raíces y la podemos escribir en forma factorizada como
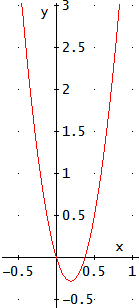
En esta sección vamos a calcular las raíces (soluciones) de ecuaciones de segundo grado completas. Para ello usaremos la fórmula cuadrática, de la que hablaremos seguidamente.
La obtención de las raíces nos permitirá descomponer o factorizar la ecuación como producto de dos polinomios de grado 1 (en caso de poder hacerlo).
Temas similares: ecuaciones de segundo grado incompletas y ecuaciones de grado mayor (Ruffini).
1. Ecuaciones completas
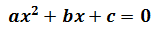
Una ecuación de segundo grado es una ecuación polinómica cuyo grado es 2,
es decir, aquella en la que el grado mayor de los monomios es 2 (es decir, su
parte literal es x2 ).
Puesto que la ecuación es de grado 2, tenemos, a lo sumo, 2
raíces (soluciones) distintas.
Toda ecuación de segunda grado se puede escribir o reducir a una ecuación
equivalente cuya forma sea:
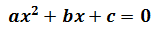
Si ninguno de los coeficientes, a,b y c es cero, es decir,
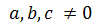
diremos que la ecuación es completa. Si no (si alguno es 0), diremos que
es incompleta.
2. Soluciones y Discriminante
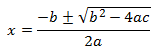
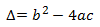
Las soluciones (o raíces) de la ecuación de segundo grado (en la forma anterior) vienen dadas por
la fórmula cuadrática:
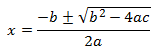
Llamamos discriminante, Δ, de la ecuación al radicando de la fórmula anterior, es decir,
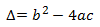
Se cumple que
-
Si Δ es 0, la ecuación tiene una única solución (de multiplicidad 2)
-
Si Δ es menor que 0, no existen soluciones (reales)
-
Si Δ es mayor que 0, existen dos soluciones (reales) distintas(de multiplicidad 1).
3. Factorización
Ejemplo:
Factorizar una ecuación consiste en expresarla como un producto de polinomios más
simples, esto es, como un producto de polinomios de grado menor.
Ejemplo:
Método para factorizar
-
Supongamos que A y B son las dos soluciones de la ecuación
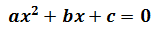
Entonces, podemos escribir el polinomio anterior (la parte izquierda) como
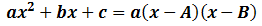
-
Si la única solución es A (por tanto, con multiplicidad 2), la factorización queda como
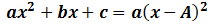
-
Si no hay soluciones, no podemos factorizar.
4. 10 ecuaciones resueltas
Ecuación 1
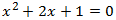
El discriminante de la ecuación es
Por tanto, la ecuación tiene una solución real doble.
Aplicamos la fórmula:
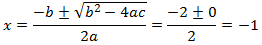
Luego la solución doble es x = -1.
Una factorización de la ecuación es
Ecuación 2
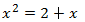
Escribimos la ecuación en la forma general:
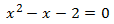
El discriminante es
Como el discriminante es positivo, la ecuación tiene dos raíces simples.
Aplicamos la fórmula para obtenerlas:
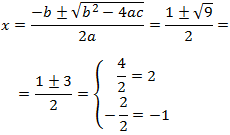
Las soluciones son x = -1, 2.
y una factorización es
Ecuación 3
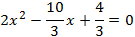
Multiplicamos por 3 la ecuación para evitar las fracciones:
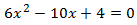
El discriminante de la ecuación es
Como Δ > 0, la ecuación tiene dos raíces simples.
Aplicamos la fórmula:
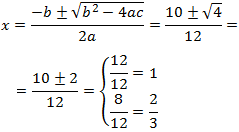
Las soluciones son
y una factorización es
Si queremos tener una igualdad entre los polinomios, tenemos que escribir el coeficiente director de
la ecuación original en la factorización:
Ecuación 4
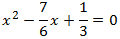
Multiplicamos la ecuación por 6 toda la ecuación para evitar las fracciones:
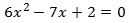
El discriminante de la ecuación es
Como el discriminante es mayor que 0, la ecuación tiene dos raíces simples. Aplicamos la fórmula
para obtenerlas:
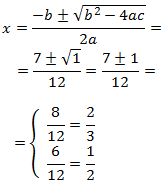
Las soluciones son
y la factorización es
Ecuación 5
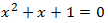
El discriminante es
Como el discriminante es negativo, la ecuación no tiene soluciones reales y, por tanto, no podemos
factorizarla.
Problema Abierto
Encontrar las raíces de la siguiente ecuación de segundo grado siendo a ≠ 0
¿Las encuentras? Puedes participar en nuestro foro.
Ecuación 6
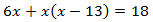
Operamos en la ecuación para escribirla en su forma general:
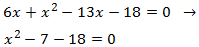
El discriminante es
Como Δ > 0, la ecuación tiene dos raíces simples.
Calculamos las raíces:
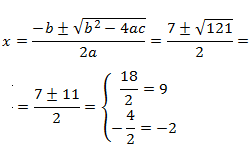
Por tanto, las soluciones son
y una factorización es
Ecuación 7
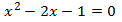
La ecuación está escrita en la forma general y su discriminante es
Como Δ > 0, existen dos raíces y son simples.
Calculamos las raíces:
Por tanto, tenemos las soluciones :
Una factorización de la ecuación es
Ecuación 8
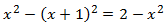
Escribimos la ecuación en la forma general. Recordemos usar la fórmula del binomio
(cuadrado de la resta):
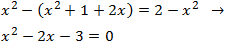
Su discriminante es
La ecuación tiene dos raíces simples ya que el discriminante es positivo.
Aplicamos la fórmula para obtenerlas:
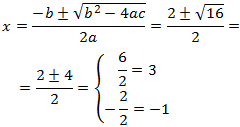
Las soluciones son
y una factorización es
Ecuación 9
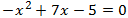
El discriminante es
Como Δ es positivo, la ecuación tiene dos soluciones simples.
Como Δ = 29, las soluciones de la ecuación será un poco complejas ya que la raíz de 29 no es exacta.
Así pues, dejaremos la raíz:
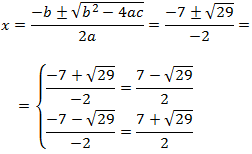
una factorización de la ecuación es
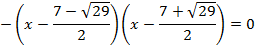
Nota: hemos multiplicado por el coeficiente director de la ecuación.
Ecuación 10 (dificultad alta)
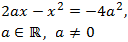
Calificamos esta ecuación como difícil por la presencia de un parámetro: a. Pero procederemos como
es habitual, la diferencia es que no sabemos qué número es a y, además, no tenemos que confundir
este parámetro con el de la fórmula cuadrática:
Supondremos que a > 0 para evitar el uso de valores absolutos.
Escribimos la ecuación en la forma general:
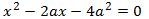
El discriminante es
El discriminante sólo puede ser positivo o cero (es cero cuando a = 0).
Como hemos supuesto que a es positivo, la ecuación tiene dos raíces simples.
Calculamos las raíces:
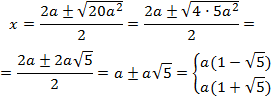
Por tanto, una factorización es
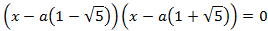
EL NUEVO MÉTODO DE PO SHEN LOH, PARA RESOLVER ECUACIONES CUADRÁTICAS.
Tomado de:
https://ecuaciones.online/de-segundo-grado/metodo-de-po-shen-loh/
Existe un nuevo método para resolver ecuaciones de segundo grado de forma rápida, siempre que el coeficiente de la variable al cuadrado sea uno, es decir, de la forma .
Desde los tiempos de los babilonios (y ya han pasado más de 4000 años) las ecuaciones cuadráticas o de segundo grado se venían resolviendo usando básicamente la famosa fórmula general para ecuaciones cuadráticas.
Pero desde finales del 2019 tenemos una alternativa, el método es del profesor chino afincado en Estados Unidos, Po-Shen Loh. Esta forma de resolver las ecuaciones de 2º grado es rápido y fácil de entender. Como vas a ver, son cuatro los pasos en los que consiste. Y ahí los tienes:
Pasos
1) Para cualquier ecuación cuadrática del tipo las soluciones están dadas por:
y ,
en donde es un número a determinar.
2) Multiplicamos entre sí estas dos soluciones y las igualamos al valor del coeficiente independiente de la ecuación de segundo grado, :
3) Resolvemos esta ecuación, hallando el valor de :
4) Cogemos la solución de la raíz positiva, y
la sustituimos en y y
listo.
Ejercicio resuelto usando Po-Shen Loh
Resuelve
1) Esta ecuación cuadrática va a tener las siguientes soluciones:
y ,
es decir:
y
en donde tenemos que encontrar el valor de .
2) Multiplicamos entre sí estas dos soluciones y las igualamos al valor del coeficiente independiente de la ecuación de segundo grado, :
3) Operando hallamos :
4) Nos quedamos con la parte positiva de la raíz, y
la sustituimos en y ,
obteniendo finalmente:
y
PROBLEMAS QUE SE RESUELVEN CON ECUACIONES DE SEGUNDO GRADO.
TOMADO DE
1. Encontrar el valor k
Determinar k de modo que en la ecuación x² − kx + 36 = 0 las raíces sean iguales.
Determinar k de modo que en la ecuación x² − kx + 36 = 0 las raíces sean iguales.
Para que las dos raíces sean iguales, el discrimnante (b² − 4ac) tiene que ser igual a cero
b² − 4ac = 0
k² − 4 · 36 = 0 k² = 144

2. Encuentra los valores que se te piden
La suma de dos números es 5 y su producto es −84. Halla dichos números.
La suma de dos números es 5 y su producto es −84. Halla dichos números.
x² − Sx + P = 0


3. Ejercicio para calcular edades
Dentro de 11 años la edad de Pedro será la mitad del cuadrado de la edad que tenía
hace 13 años.
Calcula la edad de Pedro.
Dentro de 11 años la edad de Pedro será la mitad del cuadrado de la edad que tenía
hace 13 años.
Calcula la edad de Pedro.
Designamos las variables para el ejercicio:
Edad actual x
Edad hace 13 años x − 13
Edad dentro de 11 años x + 11
Escribimos la ecuación correspondiente:

Elevamos el binomio al cuadrado, quitamos denominadores y resolvemos la ecuación


x = 7, no es una solución válida porque entonces qué edad tendría hace 13 años
Edad actual 21 años
4. Calculo de un terreno.
Para hallar una finca rectangular de 750 m² se han utilizado 110 m de cerca.
Calcula las dimensiones de la finca.
Para vallar una finca rectangular de 750 m² se han utilizado 110 m de cerca.
Calcula las dimensiones de la finca.

Semiperímetro 55
Base x
Altura 55 − x
El área es igual base por altura
x · (55 − x) = 750
Quitamos paréntesis
x² − 55x + 750 = 0
x = 25 x = 30
Las dimensiones de la finca son:
base = 30 m altura = 25 m
base = 25 m altura = 30 m
5. Rectángulos proporcionales
Los tres lados de un triángulo rectángulo son proporcionales a los números 3, 4 y 5.
Halla la longitud de cada lado sabiendo que el área del triángulo es 24 m².
Los tres lados de un triángulo rectángulo son proporcionales a los números 3, 4 y 5.
Halla la longitud de cada lado sabiendo que el área del triángulo es 24 m².

1er lado (base) 3x
2º lado (altura) 4x
3er lado 5x
Aplicamos la fórmula del área de un triángulo

Quitamos denominadores y resolvemos la ecuación

−2 no es solución porque un lado no puede tener una longitud negativa
1er lado 6 m
2º lado 8 m
3er lado 10 m
6. Calcula el área del jardín
Un jardín rectangular de 50m de largo por 34m de ancho está rodeado por un camino
de arena uniforme.
Halla la anchura de dicho camino si se sabe que su área es 540m².
Un jardín rectangular de 50 m de largo por 34 m de ancho está rodeado por un camino
de arena uniforme.
Halla la anchura de dicho camino si se sabe que su área es 540 m².

Llamaremos x a la anchura del camino
540 será igual al área total del conjunto menos el área del jardín
(50 + 2x) · (34 + 2x) − 50 · 34 = 540
Quitamos paréntesis, operamos y simplificamos la ecuación dividiendo por 4 en los
dos miembros
4x² + 168x − 540 = 0 x² + 42x − 135 = 0
x = 3 y x = −45
La anchura del camino es 3 m.
−45 no es una solución porque las distancias han de ser positivas.
7. Criterio de Semejanza en rectángulos
Calcula las dimensiones de un rectángulo cuya diagonal mide 75 m, sabiendo que
es semejante a otro rectángulo cuyos lados miden 36 m y 48 m respectivamente.
Calcula las dimensiones de un rectángulo cuya diagonal mide 75 m, sabiendo que
es semejante a otro rectángulo cuyos lados miden 36 m y 48 m respectivamente.
Base 48x : 12 = 4x
Altura 36x : 12 = 3x

(4x)² + (3x)² = 75²
25x² = 5625
x² = 225 x = 15
Base 4 · 15 = 60 m
Altura 3 · 15 = 45 m
8. Calcula el numero que se te indica
Halla un número entero sabiendo que la suma con su inverso es 25/6
Número: x
Inverso del número: 1/x

Tenemos una ecuación racional, en primer lugar tenemos que quitar denominadores



El número pedido es 5, pues 1/5 no es solución porque no es un número entero.
9. Estructura la ecuación cuadrática y calcula
Dos números naturales se diferencian en dos unidades y la suma de sus cuadrados es 580.
¿Cuáles son esos números?
Dos números naturales se diferencian en dos unidades y la suma de sus
cuadrados es 580.
¿Cuáles son esos números?
1er número x
2º número x + 2

Elevamos el binomio al cuadrado, operamos y simplificamos la ecuación
dividiendo en los dos miembros por 2



1er número 16
2º número 18
−18 no es solución porque no es un número natural
10. Calcular tiempo de llenado de una piscina
Dos caños A y B llenan juntos una piscina en dos horas, A lo hace por sí solo en tres
horas menos que B.
¿Cuántas horas tarda cada uno separadamente?
Dos caños A y B llenan juntos una piscina en dos horas, A lo hace por sí solo en tres horas menos que B.
¿Cuántas horas tarda cada uno separadamente?
Tiempo de A: x
Tiempo de B: x + 3
En una hora ocurre lo siguiente:
A= 1/X
B =1/(X+3)
Por ser una relación inversa
También sabemos que en una hora, los 2 caños juntos llenan media piscina
A + B= 1/2
Sustituimos:

Tenemos una ecuación racional, en primer lugar tenemos que quitar denominadores



Comprobamos que 3 es una solución:
Al cabo de una hora, ocurre que:
A=1/3
B=1/(3+3)=1/6
Al cabo de 2 horas:


Entonces, en 2 horas la piscina se habrá llenado 
La piscina estará completamente llena al cabo de 2 horas.
Respuesta:
Tiempo de A 3 horas
Tiempo de B 6 horas
11. Encuentra los valores que se indican
Los lados de un triángulo rectángulo tienen por medidas en centímetros tres
números pares consecutivos.
Halla los valores de dichos lados.
Los lados de un triángulo rectángulo tienen por medidas en centímetros tres
números pares consecutivos.
Halla los valores de dichos lados.

1er cateto 2x
2º cateto 2x + 2
Hipotenusa 2x + 4
Aplicamos el teorema de Pitágoras
(2x)² + (2x + 2)² = (2x + 4)²
Elevamos los binomios al cuadrado, operamos y simplificamos la ecuación
dividiendo en los dos miembros por 4
4x² + 4x² + 8x + 4 = 4x² + 16x + 16
4x² − 8x − 12 = 0 x² − 2x − 3 = 0
x = 3 y x= −1
1er cateto 6 cm
2º cateto 8 cm
Hipotenusa 10 cm
No consideramos x= −1 porque las distancias son positivas
12. Calculo de un volumen
Una pieza rectangular es 4 cm más larga que ancha.
Con ella se construye una caja de 840 cm³ cortando un cuadrado de 6 cm de lado
en cada esquina y doblando los bordes.
Halla las dimensiones de la caja.
Una pieza rectangular es 4 cm más larga que ancha.
Con ella se construye una caja de 840 cm³ cortando un cuadrado de 6 cm de lado
en cada esquina y doblando los bordes. Halla las dimensiones de la caja.

Ancho: x
Largo: 4x
Alto: 6 cm
El volumen de la caja, que es prisma rectangular, es: largo × ancho × alto
6 (x − 12) · (x + 4 −12) = 840 (x − 12) · (x −8) = 140
Pasamos el 6 dividiendo al segundo miembro y se multiplican los binomios
x² − 20x − 44 = 0 x = 22 y x = −2
Ancho: 22 cm
Largo: 26 cm
La solución −2 la rechazamos porque una longitud no puede ser negativa
13. Llenando un deposito
Un caño tarda dos horas más que otro en llenar un depósito y abriendo los dos
juntos se llena en 1 hora y 20 minutos.
¿Cuánto tiempo tardará en llenarlo cada uno por separado?
Un caño tarda dos horas más que otro en llenar un depósito y abriendo los dos
juntos se llena en 1 hora y 20 minutos.
¿Cuánto tiempo tardará en llenarlo cada uno por separado?
Tiempo del 1º x
Tiempo de 2º x − 2
1º 
El primero llena un depósito en x horas.
2º 
El segundo llena un depósito en (x − 2) horas
Pasamos el tiempo a una fracción de hora
1 hora y 20 minutos = 4/3 horas
Entre los dos 

Hacemos el inverso en el segundo miembro

Quitamos denominadores, el m.c.m. es: 4x(x − 2)


Tiempo del 1º 4 horas
Tiempo de 2º 2 horas
 no es
una solución, porque el tiempo empleado por el segundo caño sería negativo.
no es
una solución, porque el tiempo empleado por el segundo caño sería negativo.


