ECUACIONES ESPECIALES. 

 

Llamamos ecuaciones especiales a ecuaciones de grado mayor a dos que no puedan enmarcarse en el modelo cuadrático, ecuaciones con radicales o valor absoluto, en esta sección veremos estos casos.

 

Para estas ecuaciones lo primero que debemos intentar en la factorización lo que seria ideal, si esta no es posible se procederá según el caso por métodos algebraicos si no , existen otros métodos que no son tema de esta curso.

 

Una ecuación de grado superior a dos es una ecuación de cualquier grado escrita de la forma P(x) = 0.

El polinomio P(x) se puede descomponer en factores de primer y segundo grado, entonces basta igualar a cero cada uno de los factores y resolver las ecuaciones de primer grado y de segundo grado resultantes.

Ejemplo:

2x4 + x³ − 8x² − x + 6 = 0

Utilizamos el teorema del resto y la regla de Ruffini.

P(x) = 2x4 + x³ − 8x² − x + 6

Tomamos los divisores del término independiente: {±1, ±2, ±3}.

Aplicando el teorema del resto sabremos para que valores la división es exacta.

P(1) = 2 · 14 + 1³ − 8 · 1² − 1 + 6 = 2 + 1− 8 − 1 + 6 = 0

Dividimos por Ruffini.

Por ser la división exacta, D = d · c

(x −1) · (2x³ + 3x² − 5x − 6) = 0

Una raíz es x = 1.

Continuamos realizando las mismas operaciones al segundo factor.

Volvemos a probar por 1 porque el primer factor podría estar elevado al cuadrado.

P(1) = 2 · 1³ + 3 · 1² − 5x − 6≠ 0

P(− 1) = 2 · (− 1)³ + 3 · (− 1)² − 5 · (− 1) − 6= −2 + 3 + 5 − 6 = 0

(x −1) · (x +1) · (2x² +x −6) = 0

Otra raíz es x = −1.

Los otros factores lo podemos encontrar aplicando la ecuación de 2º grado.

Soluciones

x = 1, x = −1, x = 3/2, x = −2

Factorización

2(x − 1)(x + 1)(x − 3/2)(x + 2)

Ecuación cúbica:

 

Aunque en algunos casos la ecuación cubica puede resolverse según el método anterior, si no es el caso existe también una formula general para su solución que esta dada por:

 

{\displaystyle ax^{3}+bx^{2}+cx+d=0\;,\quad a\neq 0}

 

Dada la ecuación cúbica

x^3 + a_1 x^2 + a_2x + a_3 = 0

Se calculan las siguientes cantidades:

\begin{matrix} Q=\cfrac{3a_2-a_1^2}{9}, & R=\cfrac{9a_1a_2-27a_3-2a_1^3}{54} \\ \ S_1= \sqrt[3]{ R + \sqrt{Q^3+R^2} }, & S_2= \sqrt[3]{ R - \sqrt{Q^3+R^2} } \end{matrix}

En ese caso las tres raíces se pueden escribir simplemente como:

(*)\begin{cases} x_1 = S_1 + S_2 - \cfrac{a_1}{3} \ x_2 = -\cfrac{S_1+S_2}{2} - \cfrac{a_1}{3} + \cfrac{i\sqrt{3}}{2}(S_1-S_2) \ x_3 = -\cfrac{S_1+S_2}{2} - \cfrac{a_1}{3} - \cfrac{i\sqrt{3}}{2}(S_1-S_2) \end{cases}

Al ser el discriminante D = Q^3+ R^2 se tiene:

 

i) una de las raíces es real y dos de ellas son complejas si D > 0.
ii) todas las raíces son reales y al menos dos son iguales si D = 0.
iii) todas las raíces son reales y distintas si D < 0.

Se conoce como el método de Cardano, es claro que no es un método muy sencillo, sin embargo con el cuidado del caso es posible su uso.

 

ECUACIONES CON RADICALES.

 

Tomado de:

https://www.matesfacil.com/ejercicios-resueltos-ecuaciones-radicales.html

 

Método de resolución

Vamos a explicar el método de resolución a través de un ejemplo:

x−1−1=0

  1. Reordenamos la ecuación: aislamos la raíz en uno de los lados:

    x−1=1

  2. Elevamos ambos lados al orden de la raíz. Si la raíz es cuadrada,

  3. elevamos a 2; si es cúbica, elevamos a 3; si es de orden 4, elevamos a 4...

    (x−1)2=12

  4. Desarrollamos las potencias. En nuestro ejemplo, el signo radical

  5. desaparece y el cuadrado de 1 es 1:

    x−1=1

  6. Si quedan raíces, vamos de nuevo al primer paso. Si no

  7. quedan raíces, resolvemos la ecuación:

    x−1=1

    x=1+1

    x=2

  8. Comprobamos que las soluciones son realmente soluciones:

    Sustituimos x = 2 en la ecuación inicial:

    x−1−1=0

    2−1−1=0

    1−1=0

    1−1=0

    0=0

    Por tanto, x = 2 es una solución.

 

Ecuación 2

ejercicios de ecuaciones irracionales resueltos paso a paso

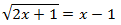
Solución

Como tenemos una raíz cuadrada, elevamos al cuadrado ambos lados de la ecuación.

No olvidemos la fórmula del cuadrado de la resta (lado derecho):

resolución de ecuaciones irracionales paso a paso. Con una o más raíces cuadradas. Secundaria, bachiller

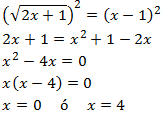
Comprobamos las soluciones:

resolución de ecuaciones irracionales paso a paso. Con una o más raíces cuadradas. Secundaria, bachiller

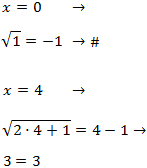
Por tanto, la única solución es x = 4.

Solución

Ecuación 3

ejercicios de ecuaciones irracionales resueltos paso a paso

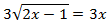
Solución

Elevamos al cuadrado ambos lados de la ecuación obteniendo una 

ecuación de segundo grado:

resolución de ecuaciones irracionales paso a paso. Con una o más raíces cuadradas. Secundaria, bachiller

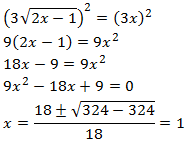
La única solución de la ecuación de segundo grado es x = 1. Comprobamos

si es la solución de la ecuación irracional:

resolución de ecuaciones irracionales paso a paso. Con una o más raíces cuadradas. Secundaria, bachiller

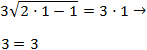
Por tanto, es solución.

 

Ecuación 4

ejercicios de ecuaciones irracionales resueltos paso a paso

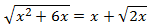
Solución

Elevamos al cuadrado para eliminar las raíces (tendremos que hacerlo dos veces)

y resolvemos la ecuación de segundo grado (factorizando):

resolución de ecuaciones irracionales paso a paso. Con una o más raíces cuadradas. Secundaria, bachiller

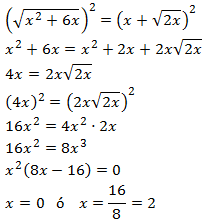
Comprobamos las soluciones:

resolución de ecuaciones irracionales paso a paso. Con una o más raíces cuadradas. Secundaria, bachiller

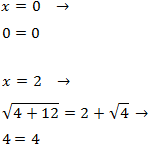
Por tanto, ambas son soluciones.

 

Ecuación 5

ejercicios de ecuaciones irracionales resueltos paso a paso

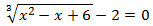
Solución

Como tenemos una raíz cúbica, elevamos al cubo ambos lados de la ecuación.

Para evitar tener que usar la fórmula del trinomio al cubo, escribimos el -2 al otro

lado de la ecuación:

resolución de ecuaciones irracionales paso a paso. Con una o más raíces cuadradas. Secundaria, bachiller

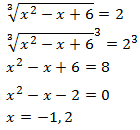
Comprobamos las soluciones:

resolución de ecuaciones irracionales paso a paso. Con una o más raíces cuadradas. Secundaria, bachiller

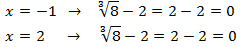
Por tanto, ambas son solución.

Solución

Ecuación 6

ejercicios de ecuaciones irracionales resueltos paso a paso

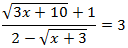
Solución

Antes de elevar al cuadrado (dos veces), multiplicamos la ecuación por el denominador para evitar las fracciones (pasamos el denominador multiplicando en el lado derecho).

resolución de ecuaciones irracionales paso a paso. Con una o más raíces cuadradas. Secundaria, bachiller

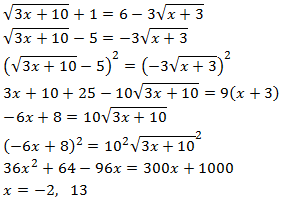
Comprobamos las soluciones:

resolución de ecuaciones irracionales paso a paso. Con una o más raíces cuadradas. Secundaria, bachiller

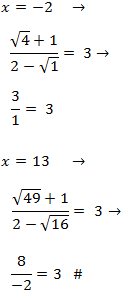
Por tanto, la única solución es x = - 2.

 

ECUACIONES CON VALOR ABSOLUTO

 

Tomado de:

http://matematicatuya.com/DESIGUALDADES/S8_Ecuaciones_Absoluto.html

 

 

Primero trataremos ecuaciones con un solo valor absoluto y la variable sólo dentro de las barras del valor absoluto como

  |x+2|=5     o    |2x−5|=7

El método que aplicaremos también puede ser extendido a ecuaciones en que la variable también está fuera del valor absoluto como

|3x+1|=x+1

 

Para resolver estas ecuaciones podemos usar la definición de un valor absoluto, tomamos en cuenta que el valor absoluto deja igual a una cantidad positiva y a una cantidad negativa le cambia el signo.

    Analicemos la primera ecuación, |x+2|=5. Existen dos posibilidades para que este valor absoluto sea igual a 5.

Primera posibilidad: Que la cantidad dentro de las barras del valor absoluto sea positiva. En este caso, como el valor absoluto a una cantidad positiva la deja igual, la ecuación quedaría x+2=5.

Segunda posibilidad: Que la cantidad entre las barras del valor absoluto sea negativa. En este caso, como el valor absoluto a una cantidad negativa le cambia de signo, la ecuación quedaría −(x+2)=5. Multiplicando por menos uno ambos lados de la ecuación obtenemos (x+2)=−5.
( Otra forma de verlo Si en |x+2|=5 la cantidad entre valor absoluto es negativa es porque su valor es menos 5 ).

Resumiendo,
la ecuación |x+2|=5 es equivalente a que x+2=−5 o bien x+2=5

Pasamos entonces a resolver las dos ecuaciones que nos conducirá al conjunto solución de la ecuación con valor absoluto.
x+2=−5x=−7 o bien  o bien x+2=5x=3
En definitiva, el conjunto solución de la ecuación con valor absoluto es {−7,3}.



 

Observe que terminamos resolviendo dos ecuaciones sin valor absoluto para encontrar el conjunto solución de la ecuación dada. Para abreviar el proceso de resolución de una ecuación con un valor absoluto, como la dada, establecemos la siguiente proposición de equivalencia:


Proposición Para c>0 tenemos

|expresio´n|=c   es equivalente a   expresio´n=−c     o     expresio´n=c



Podemos resolver algunas ecuaciones con valor absoluto aplicando esta proposición de equivalencia.

Veamos ejemplos.

Ejemplo Resolver la ecuación   |2x−5|=7.
Solución Haz clic para ver el desarrollo del paso.
 Despejar la expresión con valor absoluto en el miembro izquierdo y verificar que el otro miembro se tiene una constante positiva.

Paso 1 El valor absoluto ya está despejado. El otro miembro es una constante positiva.


 Aplicar la proposición

Paso 2 La ecuación es equivalente a
2x−5=−7 o 2x−5=−7


 Resolver las dos ecuaciones sin valor absoluto planteadas en el paso anterior.

Paso 3 Resolvemos cada ecuación
2x−5=−72x=−2x=−1ooo2x−5=72x=12x=6


 Establecer el conjunto solución.

Paso 4 El conjunto solución es {−1,6}.

 



Ejemplo Resolver la desigualdad     7−4|2−x|=−1.
Solución Haz clic para ver el desarrollo del paso.
 Despejar la expresión con valor absoluto en el miembro izquierdo y verificar que el miembro derecho es una constante positiva.

Paso 1
7−4|2−x|−4|2−x||2−x|===−1−82
El valor absoluto ya està despejado y el lado derecho es una cantidad positiva.


 Aplicar la proposición.

Paso 2 La ecuación es equivalente a
2−x=−2o2−x=2


 Resolver cada ecuación sin valor absoluto.

Paso 3 Se tiene que resolver dos ecuaciones
2−x=−2−x=−4x=4ooo2−x=2−x=0x=0


 Establecer el conjunto solución.

Paso 4 El conjunto solución es {0,4}.

 



Verdadero o Falso
La ecuación |x−3|=−6 es equivalente a

x−3=−6ox−3=6

Falso.
  No se puede aplicar la proposición de equivalencia, pues c=−6 es un número negativo.
El conjunto solución se determina analizando, un valor absoluto nunca puede ser igual a un número negativo. Por tanto, el conjunto solución es el vacio :∅.




Ecuaciones con la incógnita dentro y fuera de las barras del valor absoluto
Otros tipos de ecuaciones con el valor absoluto en un lado de la ecuación y una expresión en la variable en la otra pueden ser resueltas usando la equivalencia. Tan solo hay que tomar en cuenta que el otro lado debe ser una cantidad no negativa.




Ejemplo Encontrar el conjunto solución de la ecuación |3x+1|=x+1.
Solución Haz clic para ver el desarrollo del paso.
 Verificar que el valor absoluto esté de un lado. Establecer la condición que el lado derecho debe ser positivo o cero.
 Aplicar la proposición.

Paso 2
Para x+1≥0

|3x+1|=x+1 es equivalente a
3x+1=−(x+1)o3x+1=x+1


 Resolver las ecuaciones planteadas en el paso anterior.

Paso 3
3x+1=−(x+1)4x=−2x=−12ooo3x+1=x+12x=0x=0


 Eliminar las soluciones que no satisfacen la condición que el lado derecho debe ser positivo o cero.

Paso 4
Podemos proceder de varias maneras. Cuando se tiene ecuaciones es muy cómodo verificar si las dos soluciones satisfacen la desigualdad x+1≥0, sustituyendo
x=0 es solución de la ecuación con valor absoluto, pues para este valor la desigualdad en cierta:
0+1≥0

x=−12 es solución de la ecuación con valor absoluto, pues para este valor la desigualdad en cierta:
−12+1≥0
Observación. En este caso no se elimina ninguna solución, pues ambas hacen que la expresión del lado derecho de la ecuación sea mayor o igual a cero.


 Establecer el conjunto solución.

Paso 5
Conjunto solución ={−12,0}

 

 

En este ejemplo se tiene que las soluciones de las ecuaciones planteadas por la equivalencia son las soluciones de la ecuación con valor absoluto.

Otras situaciones se pueden presentar. Dejamos como ejercicio verificar los detalles de los siguientes.


Ejemplo El conjunto solución de la ecuación |1−4x|=2x−5 es vacio, pues las soluciones de las ecuaciones planteadas al aplicar la propiedad, x=1 y x=−2, no satisfacen la condición que el lado derecho sea positivo o cero: 2x−5≥0.


Ejemplo El conjunto solución de la ecuación |x−1|=2x+1 es {0}, ya que en las soluciones de las dos ecuaciones planteadas al aplicar la propiedad, x=−2 y x=0, se debe eliminar la solución x=−2 pues no cumple la condición que el lado derecho sea positivo o cero: 2x+1≥0. (2(−2)+1=−3<0).



Ejercicios Resuelva cada una de las siguientes ecuaciones.

1.1)|x+2|=51.3)14−2|x+2|=01.5)|x+2|+7=01.7)|x+1|=2x+11.9)∣∣x2+6x+4∣∣=41.2)|3x+1|=51.4)|x−2|=−31.6)∣∣3−x3∣∣−2=01.8)∣∣x2−9∣∣=01.10)|3x+1|+1−x=0

 Haz clic para ver las respuestas.

 

1.1)1.4)1.7)1.10){3,−7}∅{0}∅1.2)1.5)1.8){−2,43}∅{0,1}1.3)1.6)1.9){−178,−158}{−3,9}{0,−2,−4,−6}